Denote:
Ab,Ac = the reflections of A' in BB', CC', resp.
Bc,Ba = the reflections of B' in CC', AA', resp.
Ca,Cb = the reflections of C' in AA', BB', resp.
Ha, Hb, Hc = the orthocenters of the triangles A'AbAc, B'BcCa, C'CaCb, resp.
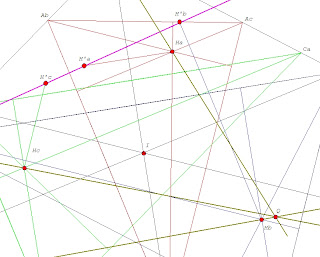
H'a, H'b, H'c = the reflections of Ha, Hb, Hc in AA', BB', CC', resp.
Conjecture 1.:
The triangles ABC, HaHbHc are perspective.
Conjecture 2.:
The points H'a, H'b, H'c are collinear
Locus of variable P such that
1. ABC, HaHbHc are perspective
2. H'a, H'b, H'c are collinear?
Antreas P. Hatzipolakis, 17 May 2013

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου