TRIANGLE CONSTRUCTION A, a + b, a + c

To construct triangle ABC if are given A, a + b, a + c

Solution 1.

Analysis:

Let ABC be the triangle in question. Let D, E be two points on the extensions of AC,AB, resp. such that CD = BE = BC = a.

The parallel from A to BC intersects DB at Z.

The triangle AZB is similar to triangle CDB ==>

AZ / AD = CB / CD = 1 ==> AZ = AD (1)

The parallel from Z to AE intersects DE at Q.

The triangles AZQ and CBE are similar ==>

AZ / ZQ = CB / BE = 1 ==> ZQ = AZ (2)

(1) /\ (2) ==> AD = AZ = ZQ (3).

The parallel from Z to EQ intersects AB at H.

We have HE = ZQ (4) (since EHZQ is parallelogram)

(3) /\ (4) ==> HE = AD.

Construction:

I construct the triangle ADE such that AD = b+a, AE = c+a, angle DAE = A.

Let H be on AE such that EH = AD.

The circle (A, AD) intersects the parallel from H to DE at Z.

The line DZ intersects AE at B. The parallel from B to AZ intersects AD at C.

ABC is the required triangle.

The Proof and Investigation are left to the reader.

Reference:
Ioannis Panakis: Solutions of the Exercises of the MATHEMATICS of the 5th Class of Greek Gymnasium, vol I, Athens, Kokotsakis Bookstore, p. 90.

Solution 2.

Analysis:

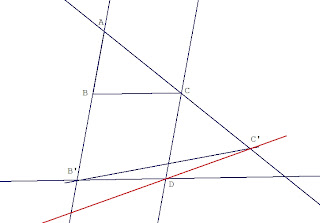
Let ABC be the triangle in question. Let B', C' be two points on the extensions of AB,AC, resp. such that BB' = CC' = BC = a.

Let D be the intersection of the lines: Parallel from B' to BC and Parallel from C to BB'. The quadrilateral BCDB' is rhombus. The isosceles triangle DCC' has fixed angles: DCC' = A, CDC' = CC'D = (90-A)/2 ("remains similar to itself"). Therefore CD/C'D is fixed, and since CD = B'D ==> B'D/C'D is fixed.

So the point D lies on a known line forming with AC' angle (90-A)/2 and on the Apollonius circle (B'C', B'D/C'D).

The Construction, Proof and Investigation are left to the reader.

Reference:
EUCLID [publ. by the Greek Mathematical Society], December 1982.

Solution 3.

Analysis:

Let ABC be the triangle in question. Let B', C' be two points on the extensions of AB,AC, resp. such that BB' = CC' = BC = a.

Let D be the intersection of BC' and CB' and E the intersection of the parallel from C' to AB' and the parallel from B' to BC'.

The isosceles trianle CC'E has fixed angles:

(CC'E) = 180 - A, (C'CE) = (C'EC) = A/2.

We have:

Angle (CB'E) = (CDC') = (CBD) + (BCD) = C/2 + B/2 = 90 - (A/2) : fixed.

Construction:

I construct the triangle AB'C' such that AB' = c+a, AC' = b+a, angle (B'AC') = A. Let L be an arbitrary point on C'A and M a point on the parallel through C' to AB' such that C'L = C'M. The circle (LM, 90-(A/2)), ie the circle with chord LM and angle 90-(A/2), intersects B'C at N. The parallel through B' to LN intersects AC' at C. The parallel through B' to MN intersects C'M at E. The parallel through C' to B'E intersects AB' at B. The triangle ABC is the required triangle.

Proof (to prove B'B = BC = CC') / Investigation: Left to the reader.

Reference: A. P. Hatzipolakis (1982)

Exercise:
Contruct the triangle if are given:
1. A, b + a, c - a
2. A, b - a, c - a