EQUILATERAL TRIANGLE

Lemma:

Let 123456 be a hexagon insrcribed in circle (0).

If the triangles 012, 034, 056 are equilateral, then the triangle with vertices the midpoints of the segments 23, 45, 61 is equilateral.

Reference:

Mathematical Chronicles (Athens), #5 (May 1969), p. 87

APH, Anopolis, #197

Application:

Let ABC be a triangle. Construct the equilateral triangle OAbAc with OA as altitude from O to base AbAc (Ab, Ac near to B, C, resp. Similarly construct the equilateral triangles OBaBc, OCaCb.

Let Ma, Mb, Mc be the midpoints of BcCb, CaAc, AbBa, resp.

The triangle MaMbMc is equilateral with center the centroid of ABC

The Ma, Mb, Mc are the centers of the equilateral A'BC, B'CA, C'AB, erected outwardly on the sides of the triangle.

The triangles ABC, MaMbMc are perspective.

The perspector is 1st Napoleon point.

Antreas P. Hatzipolakis, 30 April 2013

SIX CONCYCLIC CIRCUMCENTERS

Let ABC be a triangle, P a point, A'B'C' the cevian triangle of P wrt ABC and A"B"C" the cevian triangle of P wrt A'B'C' (ie A" = AA' /\ B'C' etc).

Denote:

A* = BC" /\ CB"

B* = CA" /\ AC"

C* = AB" /\ BA"

For which points P the circumcenters of the six triangles:

PA*B", PA*C", PB*C",PB*A", PC*A", PC*B" are concyclic?

Antreas P. Hatzipolakis, 26 April 2013

EXCENTRAL TRIANGLE

Let ABC be a triangle, IaIbIc the excentral triangle and Q the circumcenter of IaIbIc.

Denote:

Ab, A'b = the intersections of the line IaIc with the excircle (Ic) (Ab near B)

Ac, A'c = the intersections of the line IaIb with the excircle (Ib) (Ac near C)

Bc, B'c = the intersections of the line IbIa with the excircle (Ia) (Bc near C)

Ba, B'a = the intersections of the line IbIc with the excircle (Ic) (Ba near A)

Ca, C'a = the intersections of the line IcIb with the excircle (Ib) (Ca near A)

Cb, C'b = the intersections of the line IcIa with the excircle (Ia) (Cb near B)

A1, A2 = the circumcenters of IaAbAc, IaA'BA'c, resp.

B1, B2 = the circumcenters of IbBcBa, IbB'cB'a, resp.

C1, C2 = the circumcenters of IcCaCb, IcC'aC'b, resp.

1. The circles (Q),(A1),(A2) concur at a point Da

The circles (Q),(B1),(B2) concur at a point Db

The circles (Q),(C1),(C2) concur at a point Dc

Properties of the points? (Perspectivity of DaDbDc with triangles ??)

2. The circumcenters A1,A2 - B1, B2 - C1, C2 are symmetric with center of symmetry the circumcenter Q of IaIbIc. (They lie on a conic with center Q)

3. The Triangles

3.1. ABC, Bounded by (AbAc, BcBa, CaCb)

3.2. ABC, Bounded by (A'bA'c, B'cB'a, C'aC'b)

3.3. Bounded by (AbAc, BcBa, CaCb), Bounded by (A'bA'c, B'cB'a, C'aC'b)

are perspective.

Perspectors?

Antreas P. Hatzipolakis, 24 April 2013

PERSPECTIVE

Let ABC be a triangle, A'B'C' the antipedal triangle of P = O and Oa, Ob, Oc the circumcenters of OB'C', OC'A', OA'B'. resp.

Denote:

Ab = ObOa /\ OcA

Ac = OcOa /\ ObA

Bc = OcOb /\ OaB

Ba = OaOb /\ OcB

Ca = OaOc /\ ObC

Cb = ObOc /\ OaC

The triangles OaObOc, Triangle A*B*C* bounded by (AbAc, BcBa, CaCb) are perspective (??).

Locus of P ??

Antreas P. Hatzipolakis, Anopolis #156

CONCYCLIC POINTS. LOCUS

A CIRCLE:

Let ABC be a triangle, A'B'C' the cevian triangle of I and N1, N2, N3 the NPC centers of IB'C', IC'A', IA'B', resp.

The points I, N1,N2,N3 are concyclic.

ETC X(5453)

Center of the circle?

LOCUS:

Let ABC be a triangle, P a point, A'B'C' the cevian triangle of P and N1, N2, N3 the NPC centers of PB'C', PC'A', PA'B', resp.

Which is the locus of P such that the points P,N1,N2,N3 are concyclic ?

Antreas P. Hatzipolakis, 17 April 2013, Hyacinthos #21970

**********************************************************

The center X of the circle has trilinears:

2*cos(A)+4*sin(3*A/2)*cos(B/2-C/2)+ cos(B-C)+2 : :

ETC search: 2.387773069046934.., 2.38593313995937.., 0.886815506990847..

X = Midpoint of X(I),X(J) for these (I,J): (1,500)

X lies on line X(I),X(J) for these (I,J):

(1,30), (3,81), (5,581), (21,323), (58,5428), (140,3216), (186,2906), (386,549), (511,1385), (550,991), (1154,2646), (2771,3743)

Cιsar Lozada Hyacinthos #21972

**********************************************************

A related locus:

Q such that Q and the NPCs of BCQ, CAQ, ABQ are concyclic. This would include X(13), X(14), the bicentric pair PU(5), the circumcircle intercepts of line X(5)X(523), and the point Qi (of ABC) such that I = Qi of the cevian triangle of I.

Randy Hutson, Hyacinthos #21977

This is the tricircular sextic: Q014 - 4 S^2 x y z (x + y + z) (c^2 x y + b^2 x z + a^2 y z) where S = twice the area of ABC. (tricircular = the circular points are triple points of the curve).

Francisco Javier Hyacinthos #21981

.... the point Qi on this curve is the point which is the incenter of its anticevian triangle, and has ETC search value 1.999434154060428. Coordinates? Its isogonal conjugate Qi* is the point which is the nine-point center of its pedal triangle (ETC search 1.142779079509848). The line QiQi* passes through X(5).

Randy Hutson, Hyacinthos #21982

Does this locus contain any ETC centers or bicentric pairs besides X(13), X(14), and PU(5)? Are the circumcircle intercepts of line X(5)X(523) triangle centers or another bicentric pair?

Randy Hutson, Hyacinthos #21983

QUINTIC

Let ABC be a triangle, P a point and A1,B1,C1 are the NPC centers of PBC, PCA, PAB, resp.

Which is the locus of P such that the circumcenter O0 of A1B1C1 lies on the Euler line?

P : X1 = I, X4= H, X5 = N.......

For P = I we have O0 = N

Antreas P. Hatzipolakis, 15 April 2013

****************************************

It is a circular quintic through I, H and N. The other three intersection points with Euler line are X30 (the infinite point) and the instersections with the circumcircle X1113 and X1114.

Equation:

a^6 c^2 x^3 y^2 - 3 a^4 b^2 c^2 x^3 y^2 + 3 a^2 b^4 c^2 x^3 y^2 - b^6 c^2 x^3 y^2 - a^4 c^4 x^3 y^2 + a^2 b^2 c^4 x^3 y^2 - a^2 c^6 x^3 y^2 + c^8 x^3 y^2 + a^6 c^2 x^2 y^3 - 3 a^4 b^2 c^2 x^2 y^3 + 3 a^2 b^4 c^2 x^2 y^3 - b^6 c^2 x^2 y^3 - a^2 b^2 c^4 x^2 y^3 + b^4 c^4 x^2 y^3 + b^2 c^6 x^2 y^3 - c^8 x^2 y^3 + 3 a^2 b^4 c^2 x^3 y z - 3 b^6 c^2 x^3 y z - 3 a^2 b^2 c^4 x^3 y z + 3 b^2 c^6 x^3 y z + 2 a^6 c^2 x^2 y^2 z - 2 b^6 c^2 x^2 y^2 z - 4 a^4 c^4 x^2 y^2 z + 4 b^4 c^4 x^2 y^2 z + 2 a^2 c^6 x^2 y^2 z - 2 b^2 c^6 x^2 y^2 z + 3 a^6 c^2 x y^3 z - 3 a^4 b^2 c^2 x y^3 z + 3 a^2 b^2 c^4 x y^3 z - 3 a^2 c^6 x y^3 z - a^6 b^2 x^3 z^2 + a^4 b^4 x^3 z^2 + a^2 b^6 x^3 z^2 - b^8 x^3 z^2 + 3 a^4 b^2 c^2 x^3 z^2 - a^2 b^4 c^2 x^3 z^2 - 3 a^2 b^2 c^4 x^3 z^2 + b^2 c^6 x^3 z^2 - 2 a^6 b^2 x^2 y z^2 + 4 a^4 b^4 x^2 y z^2 - 2 a^2 b^6 x^2 y z^2 + 2 b^6 c^2 x^2 y z^2 - 4 b^4 c^4 x^2 y z^2 + 2 b^2 c^6 x^2 y z^2 + 2 a^6 b^2 x y^2 z^2 - 4 a^4 b^4 x y^2 z^2 + 2 a^2 b^6 x y^2 z^2 - 2 a^6 c^2 x y^2 z^2 + 4 a^4 c^4 x y^2 z^2 - 2 a^2 c^6 x y^2 z^2 + a^8 y^3 z^2 - a^6 b^2 y^3 z^2 - a^4 b^4 y^3 z^2 + a^2 b^6 y^3 z^2 + a^4 b^2 c^2 y^3 z^2 - 3 a^2 b^4 c^2 y^3 z^2 + 3 a^2 b^2 c^4 y^3 z^2 - a^2 c^6 y^3 z^2 - a^6 b^2 x^2 z^3 + b^8 x^2 z^3 + 3 a^4 b^2 c^2 x^2 z^3 + a^2 b^4 c^2 x^2 z^3 - b^6 c^2 x^2 z^3 - 3 a^2 b^2 c^4 x^2 z^3 - b^4 c^4 x^2 z^3 + b^2 c^6 x^2 z^3 - 3 a^6 b^2 x y z^3 + 3 a^2 b^6 x y z^3 + 3 a^4 b^2 c^2 x y z^3 - 3 a^2 b^4 c^2 x y z^3 - a^8 y^2 z^3 + a^2 b^6 y^2 z^3 + a^6 c^2 y^2 z^3 - a^4 b^2 c^2 y^2 z^3 - 3 a^2 b^4 c^2 y^2 z^3 + a^4 c^4 y^2 z^3 + 3 a^2 b^2 c^4 y^2 z^3 - a^2 c^6 y^2 z^3 = 0

Francisco Javier, Hyacinthos #21962

SEQUENCE OF POINTS ON THE EULER LINE

Let ABC be a triangle.

Denote:

A1, B1, C1 = The NPC centers of NBC, NCA, NAB, resp.

A2, B2 ,C2 = The NPC centers of A1BC, B1CA, C1AB, resp.

A3, B3, C3 = The NPC centers of A2BC, B2CA, C2AB

An, Bn, Cn = The NPC centers of A_n-1BC, B_n-1CA, C_n-1AB.

On = the circumcenter of the triangle AnBnCn.

The points O1, O2,......, On, ..... lie on the Euler Line of ABC.

The point O1 is now in ETC: X5501

Coordinates of On? Ratio of OnO / OnN ?

Antreas P. Hatzipolakis, 14 April 2013

********************************************

I calculated the ratios NO1:O1O and NO2:O2O. The expression for the first one is quite long, and that for the second one is enormous:

If p stands for the semiperimeter, we have

NO1:O1O = (2 p^4 - 12 p^2 r^2 + 2 r^4 - 16 p^2 r R + 16 r^3 R - 8 p^2 R^2 + 40 r^2 R^2 + 32 r R^3 + 9 R^4)/(2 p^4 + 20 p^2 r^2 + 2 r^4 - 16 p^2 r R + 16 r^3 R - 16 p^2 R^2 + 48 r^2 R^2 + 64 r R^3 + 23 R^4)

Francisco Javier, Hyacinthos #21952

The conjecture is false !!

From Cesar Lozada (24 June 2016)

Dear Antreas,

Sorry. O1 does lie on Euler line but O2 does not. Algebraically confirmed.

I didn´t try O3 because calculus are awful

Regards,

César Lozada

CIRCUMCENTER OF N1N2N3

Let ABC be a triangle, P a point and N1,N2,N3 the NPC centers of PBC, PCA, PAB, resp.

Which is the circumcenter Op of N1N2N3 ?

P = H. Op = N [N1 = N2 = N3 = N (N1N2N3 is degenerated)]

P = I. Op = N

P = O. Op lies on the line NU, where U is the Poncelet point of O wrt ABC (ie the point where concur the NPCs of OBC,OCA,OAB and ABC)

P = N. Op lies on the Euler line of ABC.

If P describes a line (Euler line, etc) which is the locus of Op?

If P describes the circumcircle, Op is the Poncelet point of P wrt ABC. If P describes other curves?

Antreas P. Hatzipolakis, 14 April 2013

********************************************************

For P = O, Op = complement of X(157).

In general, Op = complement of the nine-point-center [N'] of the antipedal triangle [A'B'C'] of P.

Randy Hutson, Hyacinthos #21963

INCENTER AND NPCs

Let ABC be a triangle.

Denote:

N1,N2,N3 = The NPC centers of IBC, ICA, IAB, resp.

N11, N22, N33 = The NPC centers of N1BC, N2CA, N3AB, resp.

1. The lines N1N11, N2N22, N3N33 are parallel to Euler Line of ABC.

2. The Circumcenter of N1N2N3 is N, the NPC center of ABC.

Synthetic Proofs?

Antreas P. Hatzipolakis, 13 April 2013

RADICAL AXES OF NPCs

Let ABC be a triangle and P,P* two isogonal conjugate points.

Denote:

Ra = the radical axis of the circles (NPC of PBC), (NPC of P*BC)

Rb = the radical axis of the circles (NPC of PCA), (NPC of P*CA)

Rc = the radical axis of the circles (NPC of PAB), (NPC of P*AB)

Ra, Rb, Rc are concurrent.

Antreas P. Hatzipolakis, 12 April 2013

CONCURRENT RADICAL AXES

1.1.

Let ABC be a triangle, A'B'C' the pedal triangle of H and A"B"C" the circumcevian triangle of H wrt A'B'C'.

Denote:

Ra = the radical axis of ((B', B'C"), (C', C'B"))

Rb = the radical axis of ((C', C'A"), (A', A'C"))

Rc = the radical axis of ((A', A'B"), (B', B'A"))

The Ra,Rb,Rc are concurrent.

Note: The radical axes of ((B", B"C'), (C", C"B')),((C", C"A'), (A", A"C')), ((A", A"B'), (B", B"A')) concur at H (all circles pass through H).

1.2.

Let ABC be a triangle, A'B'C' the pedal triangle of O and A"B"C" the circumcevian triangle of O wrt A'B'C'.

Denote:

Ra = the radical axis of ((B", B"C'), (C", C"B'))

Rb = the radical axis of ((C", C"A'), (A", A"C'))

Rc = the radical axis of ((A", A"B'), (B", B"A'))

The Ra,Rb,Rc are concurrent.

Note: The radical axes of ((B', B'C"), (C', C'B")),((C', C'A"), (A', A'C")), ((A', A'B"), (B', B'A")) concur at O (all circles pass through O).

LOCUS:

Let ABC be a triangle, P a point, A'B'C' the pedal triangle of P and A"B"C" the circumcevian triangle of P wrt A'B'C'.

Denote:

Ra = the radical axis of ((B', B'C"), (C', C'B"))

Rb = the radical axis of ((C', C'A"), (A', A'C"))

Rc = the radical axis of ((A', A'B"), (B', B'A"))

R'a = the radical axis of ((B", B"C'), (C", C"B'))

R'b = the radical axis of ((C", C"A'), (A", A"C'))

R'c = the radical axis of ((A", A"B'), (B", B"A'))

Which is the locus of P such that 1. Ra,Rb,Rc 2. R'a,R'b,R'c are concurrent?

2.1.

Let ABC be a triangle and A'B'C' the circumcevian triangle of I.

Denote:

Ra = the radical axis of ((B, BC'), (C, CB'))

Rb = the radical axis of ((C, CA'), (A, AC'))

Rc = the radical axis of ((A, AB'), (B, BA'))

The Ra, Rb, Rc are concurrent.

Note: The radical axes of ((B', B'C), (C', C'B)), ((C', C'A), (A', A'C)), ((A', A'B), (B', B'A)) concur at I (all circles pass through I)

2.2.

Let ABC be a triangle and A'B'C' the circumcevian triangle of H.

Denote:

Ra = the radical axis of ((B', B'C), (C', C'B))

Rb = the radical axis of ((C', C'A), (A', A'C))

Rc = the radical axis of ((A', A'B), (B', B'A))

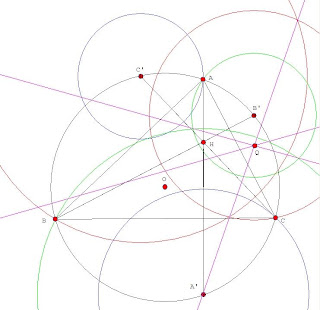
The Ra, Rb, Rc are concurrent.

Note: The radical axes of ((B, BC'), (C, CB')), ((C, CA'), (A, AC')), ((A, AB'), (B, BA')) concur at H (all circles pass through H)

LOCUS:

Let ABC be a triangle, P a point and A'B'C' the pedal triangle of P.

Denote:

Ra = the radical axis of ((B, BC'), (C, CB'))

Rb = the radical axis of ((C, CA'), (A, AC'))

Rc = the radical axis of ((A, AB'), (B, BA'))

R'a = the radical axis of ((B', B'C), (C', C'B))

R'b = the radical axis of ((C', C'A), (A', A'C))

R'c = the radical axis of ((A', A'B), (B', B'A))

Which is the locus of P such that 1. Ra,Rb,Rc 2. R'a,R'b,R'c are concurrent?

Antreas P. Hatzipolakis, 9 April 2013

***Points of Concurrence*****

1.1.

P.1.1 = (-a^2+b^2+c^2) (2 a^6 b^2-3 a^4 b^4+b^8+2 a^6 c^2+4 a^4 b^2 c^2-4 b^6 c^2-3 a^4 c^4+6 b^4 c^4-4 b^2 c^6+c^8)::

Search = -1.2087990869888377496.

On lines {{3,1568},{4,110},{5,389},{52,403},{68,1173},{155,195},{185,2072},{541,3357},{1533,5073},{1614,3153},{3167,3843},{3546,4846},{3564,3850}}

Midpoint of X(4) and X(1147).

X[3] + 2 X[4] + X[155] = 3 X[2] + 2 X[3] – X[68].

1.2.

P1.2 = (a^2-b^2-c^2) (a^4 b^4-2 a^2 b^6+b^8+2 a^2 b^4 c^2-4 b^6 c^2+a^4 c^4+2 a^2 b^2 c^4+6 b^4 c^4-2 a^2 c^6-4 b^2 c^6+c^8) :: = b^4 SB (SB^2-S^2)+c^4 SC (SC^2-S^2) ::

= complement X(1147) Search = 2.3145425702586469385

On lines {{2,54},{3,125},{5,389},{52,1594},{136,847},{155,1656},{156,542},{343,1216},{568,3574},{575,3564},{912,3812},{1614,3448},{1899,3549},{3167,5070}}

midpoint of P1.1 and P1.2 = X(5)

P1.2 = midpoint X(68) and X(1147)

P1.2 = 3 X[2] + X[68] = 3 X[2] - X[1147]

2.1

P2.1 = a (a^6-a^5 b-2 a^4 b^2+2 a^3 b^3+a^2 b^4-a b^5-a^5 c+4 a^4 b c-a^3 b^2 c-3 a^2 b^3 c+2 a b^4 c-b^5 c-2 a^4 c^2-a^3 b c^2+4 a^2 b^2 c^2-a b^3 c^2+2 a^3 c^3-3 a^2 b c^3-a b^2 c^3+2 b^3 c^3+a^2 c^4+2 a b c^4-a c^5-b c^5)::

Search = -9.3788352311451100575

On lines {{1,104},{3,10},{4,36},{5,2829},{8,2077},{21,84},{30,3829},{35,944},{40,2975},{48,1765},{56,946},{318,1309},{411,5303},{631,5251},{995,3073},{999,3671},{1006,1490},{1071,2646},{1125,3560},{1210,1470},{1385,5248},{1457,1777},{1482,4084},{2096,3485},{3072,4257},{3149,5204},{4231,5345}}

P2.1 = Midpoint of X(1) and X(1158)

P2.1 = R X[1] + (2 r - R) X[104] = (r - R) X[3] + R X[10] = (2 r + 3 R) X[21] + R X[84] = 4 r X[3] + R X[8] - R X[20]

2.2.

P2.2 = X(1147)

Peter J. C. Moses, 9 April 2013

***************************************************

ETC X5448, X5449, X5450

ORTHOLOGIC, EULER LINE

Let ABC be a triangle, A'B'C', A"B"C" the medial, orthic triangles, resp. and A*,B*,C* points on AA",BB",CC", resp. such that: A*A/A*A" = B*B/B*B" = C*C/C*C" = t.

Denote:

Ab = (Parallel to BC through A*) /\ AC

Ac = (Parallel to BC through A*) /\ AB

Bc = (Parallel to CA through B*) /\ BA

Ba = (Parallel to CA through B*) /\ BC

Ca = (Parallel to AB through C*) /\ CB

Cb = (Parallel to AB through C*) /\ CA

1. Oa, Ob, Oc = the circumcenters of A'AbAc, B'BcBa, C'CaCb, resp.

The triangles ABC, OaObOc are orthologic

The locus of the orthologic center (OaObOc, ABC), as t varies, is the Euler line of ABC.

Which is the locus of the other orthologic center (ABC, OaObOc)?

2. Na, Nb, Nc = the NPCs centers of A'AbAc, B'BcBa, C'CaCb, resp.

The triangles ABC, NaNbNc are orthologic

The locus of the orthologic center (NaNbNc, ABC), as t varies, is the Euler line of ABC.

Which is the locus of the other orthologic center (ABC, NaNbNc)?

Antreas P. Hatzipolakis, 6 April 2013

ORTHOPOLAR CIRCLES [orthic triangle]

Let ABC be a triangle and A'B'C' the orthic triangle.

Denote:

Ab,Ac = the reflections of A' in BB',CC', resp.

Bc,Ba = the reflections of B' in CC',AA', resp.

Ca,Cb = the reflections of C' in AA',BB', resp.

Let L be a line passing through H.

Denote:

0 = the orthopole of L wrt A'B'C'

1 = the orthopole of L wrt A'AbAc

2 = the orthopole of L wrt B'BcBa

3 = the orthopole of L wrt C'CaCb

The points 0,1,2,3 are concyclic.

Special Case: L = Euler line of ABC.

L passes through the common circumcenter of the triangles A'AbAc, B'BcBa, C'CaCb [= the H of ABC] and the circumcenter of A'B'C' [=the N of ABC]. The points 0,1,2,3 coincide with the Poncelet point U of H wrt A'B'C'. (The U is the point of concurrence of 7 NPCs: The NPCs of A'B'C', HB'C', HC'A', HA'B', A'AbAc, B'BcBa, C'CaCb.)

Problem:

Which is the locus of the centers of the circles 0123 as L moves around H?

Antreas P. Hatzipolakis, 6 April 2013

AN ORTHOPOLAR LINE

THEOREM (proof?):

Let ABC, A'B'C' be two triangles inscribed in two concentric circles such that A,B,A',B' are collinear. [the triangles share the same circumcenter and a midpoint of a side]

Let L be a line passing through O, the common circumcenter of the circles.

Denote:

1 = the orthopole of L wrt ABC

2 = the orthopole of L wrt A'B'C'

The line 12 passes through the intersection point of the NPCs (N),(N') of ABC, A'B'C', resp. other than the common midpoint M of AB, A'B'.

COROLLARY.

Let ABC be a triangle and A'B'C' the orthic triangle.

Denote:

Ab, Ac = the reflections of A in C',B', resp.

Bc, Ba = the reflections of B in A',C', resp.

Ca, Cb = the reflections of C in B',A', resp.

The NPCs of AAbAc, BBcBa, CCaCb are concurrent.

The point of concurrence is X1986 in ETC.

Let L be a line passing through H.

Denote:

1 = the orthopole of L wrt AAbAc

2 = the orthopole of L wrt BBcBa

3 = the orthopole of L wrt CCaCb

The points 1,2,3, X1986 are collinear.

We have:

The three triangles AAbAc, BBcBa, CCaCb share the same circumcenter, the H of ABC

A' is the midpoint of BBc of BBcBa and CCb of CCaCb ==> X1986, 2, 3 are collinear.

B' is the midpoint of CCa of CCaCb and AAc of AAbAc ==> X1986, 3, 1 are collinear.

C' is the midpoint of AAb of AAbAc and BBa of BBcBa ==> X1986, 1, 2 are collinear.

Therefore 1,2,3, X1986 are collinear

Antreas P. Hatzipolakis, 4 April 2013