The NPC center of N1N2N3 lies on the Euler line of ABC.
Antreas P. Hatzipolakis, 30 May 2013
***************************************************** The barycentric coordinates of the NPC center of N1N2N3 are:
( 2a^10 - 5a^8(b^2+c^2) + 2a^6(b^4+5b^2c^2+c^4) + a^4(4b^6-5b^4c^2-5b^2c^4+4c^6) - a^2(b^2-c^2)^2(4b^4+5b^2c^2+4c^4) + (b^2-c^2)^4(b^2+c^2) : ... : ...)
with (6-9-13)-search number: 4.7800096839999025703058
Angel Montesdeoca, Anopolis #331
Let ABC be a triangle and A'B'C' the cevian triangle of I.
Denote:
L11 = the perpendicular line to AA' at A'
L22 = the perpendicular line to BB' at B'
L33 = the perpendicular line to CC' at C'
(ie the lines L11,L22,L33 bound the antipedal triangle of I wrt A'B'C')
L12 = the reflection of L11 in BB'
L13 = the reflection of L11 in CC'
M12 = the parallel to L12 through B'
M13 = the parallel to L13 through C'
A" = line M12 /\ line M13
Similarly B" and C".
O1 = the circumcenter of the triangle A"B'C'
O2 = the circumcenter of the triangle B"C'A'
O3 = the circumcenter of the triangle C"A'B'
Conjecture 1:
The points I, O1, O2, O3 are concyclic. Center of the circle?
Conjecture 2: The circumcircles (O1), (O2), (O3) are concurrent. Point?
Antreas P. Hatzipolakis, 29 May 2013
********************************************************
The points I, O1, O2, O3 are concyclic. Center of the circle (barycentrics)
( a(b+c)(a^5-2a^3(b^2+c^2) + a(b^4-b^2c^2+c^4) - a^2b c(b+c)+ b(b-c)^2c(b+c) ) : ... : ... ).
The circumcircles (O1), (O2), (O3) are concurrent.
Point of concurrence:
( a(a^6-a^5(b+c) - a^4(b+c)^2 + (b^2-c^2)^2(b^2+c^2) + a^3(2b^3+b^2c+b c^2+2c^3) - a^2(b^4-b^3c-3b^2c^2-b c^3+c^4) - a(b^5+b^4c+b c^4+c^5)) : ... : ... )
Angel Montedeoca, Anopolis #327
Points X(5496), X(5497) in ETC
Let ABC be a triangle and A'B'C' the cevian triangle of I.
Denote:
L11 = the perpendicular line to AA' at A'
L22 = the perpendicular line to BB' at B'
L33 = the perpendicular line to CC' at C'
(ie the lines L11,L22,L33 bound the antipedal triangle of I wrt A'B'C')
L12 = the reflection of L11 in BB'
L13 = the reflection of L11 in CC'
L21 = the reflection of L22 in AA'
L23 = the reflection of L22 in CC'
L31 = the reflection of L33 in AA'
L32 = the reflection of L33 in BB'
O1 = the circumcenter of the triangle bounded by the lines (L11,L12,L13)
O2 = the circumcenter of the triangle bounded by the lines (L21,L22,L23)
O3 = the circumcenter of the triangle bounded by the lines (L31,L32,L33)
Conjecture 1:
O1, O2, O3 and O [circumcenter of ABC] are concyclic.
Denote:
Oa = the circumcenter of the triangle bounded by the lines (L11,L21,L31)
Ob = the circumcenter of the triangle bounded by the lines (L12,L22,L32)
Oc = the circumcenter of the triangle bounded by the lines (L13,L23,L33)
Conjecture 2:
The circumcenter of the triangle OaObOc is the I.
Antreas P. Hatzipolakis, 28 May 2013
*******************************************************
Conjecture 1:
Yes, O1, O2, O3 and O are concyclic. The center of the circle is:
( a^2 ( a^7 (b + c) - a^6 (b^2 + c^2) - a^5 (3 b^3 + 2 b^2 c + 2 b c^2 + 3 c^3) + a^4 (3 b^4 - b^3 c + 4 b^2 c^2 - b c^3 + 3 c^4) + a^3 (3 b^5 + b^4c + 2 b^3c^2 + 2 b^2 c^3 + b c^4 + 3 c^5) - a^2 (3 b^6 - 2 b^5 c - 2 b c^5 + 3 c^6) - a (b^7 - b^4 c^3 - b^3 c^4 + c^7) + (b^2-c^2)^2(b^4 - b^3 c - b^2 c^2 - b c^3 + c^4)):... :...),
with (6-9-13)-search number: 0.025111873257385778374122883
Angel Montesdeoca, Anopolis #321
Point X(5495) in ETC
Let La, Lb, Lc be three lines, A,B,C three respective points and 1,2,3 three respective lines.
Denote:
rLa, rLb, rLc = the reflections of La, Lb, Lc in 1,2,3, resp.
pLa, pLb, pLc = the parallels to La, Lb, Lc through A, B, C, resp.
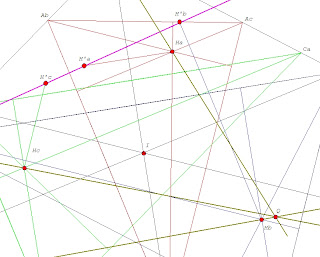
CONCURRENT EULER LINES.
Let ABC be a triangle and A'B'C' the cevian triangle I.
Denote:
Ab,Ac: = the reflections of A' in BB', CC', resp.
Bc,Ba: = the reflections of B' in CC', AA', resp.
Ca,Cb: = the reflections of C' in AA', BB', resp.
1,2,3: = the cevians AA', BB', CC' of I (bisectors)
1. L, La,Lb,Lc: = the Euler lines of ABC, AAbAc, BBcBa, CCaCb, resp.
1.1. La,Lb,Lc concur at the infinity point of L = X30 (ie L, La,Lb,Lc are parallel)
1.2. rLa, rLb, rLc are concurrent.
1.3. prLa, prLb, prLc are concurrent at a point on the circumcircle. The point is the antipode of the Euler line reflection point (ie the point of concurrence of the reflections of the Euler in the sidelines of ABC) = the isogonal conjugate of the infinity point of the Euler line (X30) = X74.
2. Da, Db, Dc: = the Euler lines of the triangles A'AbAc, B'BcBa, C'CaCb, resp.
2.1. Da, Db, Dc are concurrent at I. (I is the common circumcenter of the triangles)
2.2. pDa, pDb, pDc are concurrent.
Antreas P. Hatzipolakis, 24-25 May 2013
******************************************
1.2
The lines intersect at:
( a(a^9 - a^8(b+c) - a^7(b-c)^2 + a^6(2b^3-b^2c-b*c^2+2c^3) - a^5(3b^4+b^3c-7b^2c^2+b*c^3+3c^4) + 4a^4b*c(b-c)^2(b+c) + a^3(b^2-c^2)^2(5b^2-4b*c+5c^2) - a^2(b-c)^2(2b^5+5b^4c+b^3c^2+b^2c^3+5b*c^4+2c^5) - a(b^2-c^2)^2(2b^4-3b^3c+5b^2c^2-3b*c^3+2c^4) + (b-c)^4(b+c)^3(b^2+c^2)) : ... : ...),
with (6-9-13)-search number: 5.63864638926896001044233914
Angel Montesdeoca Anopolis, #301
On lines {{1,2779},{21,104},{36,1725},{65,74},{125,860}}
(2 r + R) X[110] - 4 (r + R) X[1385]
2 R X[65] + (2 r + R) X[74]
Peter Moses 27 May 2013
2.2
The lines are concurrent in X(80), reflection of incenter in Feuerbach point.
Angel Montesdeoca Anopolis, #308
Denote:
Iab, Iac = the excenters of IBC respective to angles PBC, PCB.
Ibc, Iba = the excenters of ICA respective to angles PCA, PAC.
Ica, Icb = the excenters of IAB respective to angles PAB, PBA.
For P = O, the six excenters are concyclic, lying on the circumcircle (O).
Are they always lying on a conic? And for which points P the conic is circle?
Denote:
Oa, O'a = the circumcenters of PIbcIcb, PIbaIca, resp.
Ob, O'b = the circumcenters of PIcaIac, PIcbIab, resp.
Oc, O'c = the circumcenters of PIabIba, PIacIbc, resp.
The triangles OaObOc, O'aO'bO'c are perspective.
The line segments OaO'a, ObO'b, OcO'c are bisected by the perspector P' of the triangles, therefore the six points lie on a conic with center P'.
For which points P the conic is circle?
Antreas P. Hatzipolakis, 20 May 2013
Denote:
(N1),(N2), (N3) = the NPCs of IBC, ICA, IAB, resp.
(12), (13) = the reflections of (N1) in BI, CI, resp.
(23), (21) = the reflections of (N2) in CI, AI, resp.
(31), (32) = the reflections of (N3) in AI, B1, resp.
The six centers 12,13,23,21,31,32 are concyclic.
The circle has diameter IO.
Perspectivity:
The circles (I), (21), (31) concur at a point A'.
The circles (I), (32), (12) concur at a point B'.
The circles (I), (13), (23) concur at a point C'.
The triangles ABC, A'B'C' are perspective (??)
Antreas P. Hatzipolakis, 19 May 2013
********************************************
Midpoint of OI = X(1385)
12 = {a (a^2-b^2+a c-2 b c-c^2),-a^3+a b^2+a^2 c+2 a b c-2 b^2 c+a c^2-3 b c^2-c^3,-c^2 (b+c)} 13 = {a (a^2+a b-b^2-2 b c-c^2),-b^2 (b+c),-a^3+a^2 b+a b^2-b^3+2 a b c-3 b^2 c+a c^2-2 b c^2}
ETC points on the Anopolis circle {1,3,1083,3109,3110}
The orthogonal projection of I on a line through O is also on the circle .. hence X(3109) & X(3110). So too X(1083) as it is the orthogonal projection of I on line X(3) X(667)
Also the orthogonal projection of O on a line through I is also on the circle
A non ETC point on the Anopolis circle
a^2 (a^4 b^2-a^2 b^4-2 a^4 b c+a b^4 c+a^4 c^2+a^2 b^2 c^2-b^3 c^3-a^2 c^4+a b c^4) ::
on lines {{1,667},{3,238},{35,1083},{41,813}}
A’ = reflection of midpoint of AI in 21 31 = {(a-b-c) (b-c)^2 (a+b-c) (a-b+c),-(a-b)^2 b^2 (a+b-c),-(a-c)^2 c^2 (a-b+c)}
A’B’C’ is perspective to ABC at X(59)
Also to the tangential triangle at:
a^2 (a^9-3 a^8 b+8 a^6 b^3-6 a^5 b^4-6 a^4 b^5+8 a^3 b^6-3 a b^8+b^9-3 a^8 c+12 a^7 b c-12 a^6 b^2 c-12 a^5 b^3 c+30 a^4 b^4 c-12 a^3 b^5 c-12 a^2 b^6 c+12 a b^7 c-3 b^8 c-12 a^6 b c^2+33 a^5 b^2 c^2-21 a^4 b^3 c^2-21 a^3 b^4 c^2+33 a^2 b^5 c^2-14 a b^6 c^2+2 b^7 c^2+8 a^6 c^3-12 a^5 b c^3-21 a^4 b^2 c^3+48 a^3 b^3 c^3-21 a^2 b^4 c^3-4 a b^5 c^3+2 b^6 c^3-6 a^5 c^4+30 a^4 b c^4-21 a^3 b^2 c^4-21 a^2 b^3 c^4+18 a b^4 c^4-2 b^5 c^4-6 a^4 c^5-12 a^3 b c^5+33 a^2 b^2 c^5-4 a b^3 c^5-2 b^4 c^5+8 a^3 c^6-12 a^2 b c^6-14 a b^2 c^6+2 b^3 c^6+12 a b c^7+2 b^2 c^7-3 a c^8-3 b c^8+c^9)::
= (2r - R) (r^2 + 6 r R + 8 R^2 - s^2) X[1486] – 4 r (r^2 + 5 r R + 4 R^2 - s^2) X[1618]
On line {1486, 1618}
Search = 0.89807482985690351940
Peter J. C. Moses, 19 May 2013
Denote:
PQa = the isogonal conjugate of P wrt QBC
PQb = the isogonal conjugate of P wrt QCA
PQc = the isogonal conjugate of P wrt QAB
QPa = the isogonal conjugate of Q wrt PBC
QPb = the isogonal conjugate of Q wrt PCA
QPc = the isogonal conjugate of Q wrt PAB
Apq = PQaQPa /\ BC
Bpq = PQbQPb /\ CA
Cpq = PQcQPc /\ AB
Conjecture: The points Apq, Bpq, Cpq are collinear.
Let R be another point. We have the lines (if the conjecture is true):
ApqBpqCpq, AqrBqrCqr, ArpBrpCrp.
Are they concurrent? Do they bound a triangle in perspective with ABC?
Antreas P. Hatzipolakis, 18 May 2013
Denote:
Ab,Ac = the reflections of A' in BB', CC', resp.
Bc,Ba = the reflections of B' in CC', AA', resp.
Ca,Cb = the reflections of C' in AA', BB', resp.
Ha, Hb, Hc = the orthocenters of the triangles A'AbAc, B'BcCa, C'CaCb, resp.
H'a, H'b, H'c = the reflections of Ha, Hb, Hc in AA', BB', CC', resp.
Conjecture 1.:
The triangles ABC, HaHbHc are perspective.
Conjecture 2.:
The points H'a, H'b, H'c are collinear
Locus of variable P such that
1. ABC, HaHbHc are perspective
2. H'a, H'b, H'c are collinear?
Antreas P. Hatzipolakis, 17 May 2013
1. The Euler line of NaNbNc is the line INF of ABC (O of NaNbNc = N of ABC, H of NaNbNc = I of ABC, F of ABC = ?? of NaNbNc).
2. The circumcircles (Oa),(Ob),(Oc) of NaBC, NbCA, NcAB, resp. concur at a point Q on the circumcircle of NaNbNc.
Which point is the Q wrt 1. ABC 2.NaNbNc ?
Antreas P. Hatzipolakis, 17 May 2013
Denote:
Ab,Ac = the reflections of A' in BB', CC', resp.
Bc,Ba = the reflections of B' in CC', AA', resp.
Ca,Cb = the reflections of C' in AA', BB', resp.
Na, Nb, Nc = The NPC centers of A'AbAc, B'BcBa, C'CaCb, resp.
O* = The circumcenter of NaNbNc. It is the NPC center of A'B'C'.
R* = the radical center of (Na), (Nb), (Nc)
The NPC circles (Na), (Nb), (Nc) concur on the NPC of A'B'C'. The point of concurrence, the R*, is the Poncelet point of H wrt A'B'C' and since the H of ABC is the I of A'B'C', the point is the Feuerbach point [1] of A'B'C' = the center of the Feuerbach hyperbola of A'B'C'.
The points R*, H, O* are collinear. The line is the INF-line of A'B'C'
Generalization:
Let P = point on the Euler line of ABC.
Conjecture:
The points R*, P, O* are collinear.
Locus:
P = a variable point.
Which is the locus of P such that R*,P,O* are collinear?
Euler Line + ???
Is the incenter I on the locus?
Note [1]:
The Feuerbach point of ABC:
Let ABC be a triangle and A'B'C' the cevian triangle of I. Denote:
Ab, Ac = the reflections of A in BB', CC', resp.
Bc, Ba = the reflectuons of B in CC', AA', resp.
Ca, Cb = the reflections of C in AA', BB', resp.
The NPCs of AAbAc, BBcBa, CCaCb (and ABC) concur at Feuerbach point of ABC.
Antreas P. Hatzipolakis, 16 May 2013
Conjecture 1:
The points I, N',I' are collinear.
Conjecture 2:
Let A"B"C" be the pedal triangle of I' wrt A'B'C'.
I' is the NPC center A"B"C".(Randy Hutson)
The line II' is the Euler line of A"B"C"
Antreas P. Hatzipolakis, 15 May 2013
Anopolis #255 (Re: NPC center of the cevian triangle of I)
Let P = (x:y:z) be a point on the Euler line of ABC.
Denote:
P1, P2, P3 = the P-points of the triangles A'B"C", B'C"A", C'A"B", resp. ie P1 = (x:y:z) wrt A'B"C", P2 = (x:y:z) wrt B'C"A", P3 = (x:y:z) wrt C'A"B". Or alternatively, since the triangles share the same circumcenter, which is the NPC center N of ABC: NP1/NH1 = NP2 / NH2 = NP3 / NH3 = t (where H1,H2,H3 are the orthocenters of the triangles A'B"C", B'C"A", C'A"B")
P'1, P'2, P'3 = the P-points of the triangles A"B'C', B"C'A', C"A'B', resp.
The circumcenter of P1P2P3 is N, the common circumcenter of the triangles.
The triangles P1P2P3, P'1P'2P'3 are perspective and inscribed in a r. hyperbola with center the perspector of the triangles.
Locus:
As P moves on the Euler Line (or t varies) which is the locus of the perspector?
Antreas P. Hatzipolakis, 13 May 2013
Denote:
G1,G2,G3 = the centroids of A'B"C", B'C"A", C'A"B", resp.
g1,g2,g3 = the centroids of A"B'C', B"C'A', C"A'B', resp.
The circumcenter of the circle (G1G2G3) is the common circumcenter of A'B'C' and A"B"C", the N of ABC.
The circle (G1G2G3) passes through G.
1. The triangles G1G23, g1g2g3 are perspective.
The six centroids lie on a conic (rectangular hyperbola) with center P, the perspector of the triangles.
2. The NPC centers of the triangles G1g2g3, G2g3g1, G3g1g2, G1G2G3, g1g2g3 concur at P (center of the hyperbola)
Antreas P. Hatzipolakis, 12 May 2013
Denote: H1,H2,H3 = the orthocenters of A'B"C", B'C"A", C'A"B", resp.
h1,h2,h3 = the orthocenters of A"B'C', B"C'A', C"A'B', resp.
H1,H2,H3, H are concyclic. The center of the circle is the common circumcenter of A'B'C' and A"B"C", the N of ABC.
1. The triangles H1H2H3, h1h2h3 are perspective.
The six orthocenters lie on a conic (rectangular hyperbola) with center P, the perspector of the triangles.
2. Denote: O1,O2,O3 = the circumcenters of H1h2h3, H2h3h1, H3h1h2, resp.
The triangles A'B'C', O1O2O3 are perspective.
3. The NPC centers of the triangles H1h2h3, H2h3h1, H3h1h2, H1H2H3, h1h2h3 concur at P (center of the hyperbola)
Antreas P. Hatzipolakis, 12 May 2013
*********************************
1. The triangles H1H2H3, h1h2h3 are perspective. The six orthocenters lie on a conic (rectangular hyperbola) with center P, the perspector of the triangles.
P=X(389), CENTER OF THE TAYLOR CIRCLE.
2. Denote: O1,O2,O3 = the circumcenters of H1h2h3, H2h3h1, H3h1h2, resp.
The triangles A'B'C', O1O2O3 are NOT perspective.
Another case:
Denote: o1,o2,o3 = the circumcenters of h1H2H3, h2H3H1, h3H1H2, resp.
The triangles A"B"C", o1o2o3 are perspective, witn perspector X(52)= ORTHOCENTER OF ORTHIC TRIANGLE.
Angel Montesdeoca, 13 May 2013
Let ABC be a triangle and P a point.
Denote:
A1, B1, C1 = The NPC centers of PBC, PCA, PAB, resp.
r11,r12,r13 = the radical axes of the NPCs: ((B1),(C1)), ((C1),(A1)), ((A1),(B1)), resp.
R1 = the point of concurrence of r11,r12,r13 [Radical center of the circles. It is the Poncelet point of P wrt ABC, lying on the NPC of ABC]
f11, f12, f13 = the parallels to r11, r12, r13 through A,B,C, resp.
The lines f11, f12, f13 concur at a point F1.
F1 is the reflection of P in R1.
Locus:
As P moves on a line (the Euler line, for example) which is the locus of F1 ?
Sequences of Ri, Fi:
Denote:
A2,B2,C2 = the NPC centers of A1BC, B1CA, C1AB, resp.
r21,r22,r23 = the radical axes of the NPC: ((B2),(C2)), ((C2),(A2)), ((A2),(B2)), resp.
R2 = the point of concurrence of r21,r22,r23
f21, f22, f23 = the parallels to r21, r22, r23 through A,B,C, resp.
The lines f21, f22, f23 concur at a point F2.
Similarly R3,R4...., Rn and F3,F4,.... Fn.
Where are lying the points Ri, Fi ?
Special points P: P = N, I
Antreas P. Hatzipolakis, 9 May 2013
The circumcenter O0 of A1A2A3 is N of ABC and the orthocenter H0 of A1A2A3 is I of ABC.
Which point wrt A1A2A3 is the Feuerbach point F of ABC (it lies on the Euler line of A1A2A3) ?
Antreas P. Hatzipolakis, 5 May 2013
Morley configuration has more miracles per square meter than any other configuration of triangle geometry.
(Antreas)
*************************
Let ABC be a triangle, A'B'C' the internal Morley Triangle and A"B"C" the adjunt triangle.
1. TRISECTORS OF BA'C, CB'A, AC'B:
Trisectors of BA'C:
AbA'bA"b with Ab on BC near B, A'b on AC, A"b on AB
AcA'cA"c with Ac on BC near C, A'c on AB, A"c on AC
Similarly the trisectors of CB'A, AC'B.
1.1. Denote:
A1 = AbBc /\ AcCb
A2 = BaCb /\ CaBc
Similarly B1,B2 and C1, C2.
Conjecture 1:
The lines A1A2,B1B2,C1C2 are concurrent (at a point P1).
Antreas P. Hatzipolakis, Anopolis #213
_____________________
The lines are concurrent, at a non-ETC point (search 1.372808061836111). I could not find any collinearities with existing Morley-related centers.
Also, the points Ab, Ac, Bc, Ba, Ca, Cb all lie on a common ellipse, with center at non-ETC point (search 1.839251887562039) and perspector at non-ETC point (search 1.102316990783906). I also could find non collinearities with these centers.
Randy Hutson Anopolis #217
_____________________
1.2. Denote:
A'1 = A'bB'c /\ A'cC'b
A'2 = B'aC'b /\ C'aB'c
Similarly B'1,B'2 and C'1, C'2.
Conjecture 2:
The lines A'1A'2,B'1B'2,C'1C'2 are concurrent (at a point P2).
The points A'b, A'c, B'c, B'a, C'a, C'b lie on a conic.
1.3. Denote:
A"1 = A"bB"c /\ A"cC"b
A"2 = B"aC"b /\ C"aB"c
Similarly B"1,B"2 and C"1, C"2.
Conjecture 3:
The lines A"1A"2,B"1B"2,C"1C"2 are concurrent (at a point P3).
The points A"b, A"c, B"c, B"a, C"a, C"b lie on a conic.
Antreas P. Hatzipolakis, 4 May 2013
Denote:
A1 = AbBc /\ AcCb
A2 = BaCb /\ CaBc
Similarly B1,B2 and C1, C2.
Conjecture:
The lines A1A2,B1B2,C1C2 are concurrent.
Antreas P. Hatzipolakis, 3 May 2013
Conjecture 2: The same for A'B'C' = the adjunct triangle.
Antreas P. Hatzipolakis, 4 May 2013
Denote:
Ab = (IBC) /\ ((I,IB)-B)
ie the other than B intersection of the circumcircle of IBC and the circle centered at I with radius IB
Ac = (IBC) /\ ((I,IC)-C)
ie the other than C intersection of the circumcircle of IBC and the circle centered at I with radius IC
Similarly:
Bc, Ba and Ca, Cb
A" = BcBa /\ CaCb
B" = CaCb /\ AbAc
C" = AbAc /\ BcBa
A'B'C' and A"B"C" are perspective. The perspector S is on the OI line, the internal center of similitude of (O) and (I) = X(55).
Denote:
Ra = the radical axis of (IBC), (I,IA)
ie the radical axis of the circumcircle of IBC and the circle centered at I with radius IA.
Similarly Rb, Rc.
A* = AbAc /\ Ra
B* = BcBa /\ Rb
C* = CaCb /\ Rc
The triangles ABC, A*B*C* are perspective at a point P on the circumcircle of ABC.
The point is the center of the Jerabek hyperbola of the antipedal triangle of I (lying on the NPC of the antipedal of I = circumcircle of ABC)
Orthic triangle variation:
Internal center of similitude of circumcircle of orthic [=NPC of ABC] and incircle of orthic [=pedal circle of incenter of orthic = H of ABC] on the Euler line of ABC.
Perspector P lies on the NPC and is the center of the Jerabek hyperbola, X(125).
Antreas P. Hatzipolakis, 2 May 2013
