TRIANGLE CONSTRUCTION A, h_b+a, h_c+a

To construct triangle ABC if are given A, h_b + a, h_c + a, where h_b,h_c are the altitudes from B,C, resp.

Solution 1

We have:

2Rh_b = ac
2Rh_c = ab

==>

h_b + a = (ac/2R) + a = (a/2R).(2R + c)

h_c + a = (ab/2R) + a = (a/2R).(2R + b)

We have that angle A is known ==> a/2R is known

[Geometric Proof:

Let O be the circumcenter and M the midpoint of BC.
The triangle BOC has known angles since A is known ==>

MC / OC is known ==> (a/2)/R = a/2R is known].

So the problem is equivalent to construct triangle if are given A, 2R + b, 2R + c.

Analysis:

Let ABC be the triangle in question, AOD diameter of the circumcircle and B',C' points on the extensions of AB,AC such that BB' = CC' = AD [= 2R].

A is known

AB' = AB + BB' = c + 2R, known

AC' = AC + CC' = b + 2R, known

==> The triangle AB'C' can be constructed.

We have:

DB is perpendicular to AB' (since AD is diameter) and BB' = AD [=2R]

==> the locus of D is the parabola with focus A and directrix the perpendicular to AB' at B' (see LEMMA).

Similarly:

DC is perpendicular to AC' and CC' = AD ==> the locus of D is the parabola with focus A and directric the perpendicular to AC' at C'.

Therefore D is intersection point of the two loci. B,C are the (other than A) intersections of the circle of diameter AD with the lines AB',AC' resp.

LEMMA:

In triangle ABC, let BC be fixed and D the orthogonal projection of A on BC. If BD = AC then the locus of A is a parabola.

Let A' be the orthogonal projection of A on the perpendicular to BC at B. We have AC = BD and BD = AA' ==> AC = AA' ==> the locus of A is the parabola with focus C and directrix the perpendicular to BC at B.

Solution 2

Let BB' = h_b, CC' = h_c be the altitudes from B,C, resp.

The right triangles C'AC,B'AB are similar and have known angles (since A is known)

==>

CC' / CA = BB' / BA is known ==>

h_c / b = h_b / c = (h_c - h_b) / (b - c) = [(h_c + a) - (h_b + a)] / (b - c)

==> b - c is known.

So the problem is equivalent to construct triangle if are given A, b - c, h_c + a.

Analysis:

Let ABC be the triangle in question with AC > AB.

Let D be the point on AC between A and C such that AD = AB, CE the altitude from C, and Z the intersection of the lines BD and CE.

In the triangle CDZ we have:

CD = AC - AD = b - c, known.

Angles (BDC) = (DAB) + (DBA) = A + (90 - (A/2)) = 90 + (A/2), known

(DCZ) = 90 - (CAE) = 90 - A, known.

Therefore the triangle CDZ can be constructed.

Let H be the point on the extension of CE such that EH = BC.

We have CH = CE + EH = h_c + a, known.

BE is perpendicular to CH and BC = EH ==> (according to LEMMA) the locus of B is the parabola with focus C and directrix the perpendicular to CH at H.

So B is the intersection of the line DZ and the parabola.

Solution 3

Let ABC be the triangle in question and O its circumcenter.

The perpendicular bisector of BC intersects the circumcircle at D,E (as in the figure).

Denote:

CD = DB =: m

EC = EB =: n

AD := d

EA := e

We have:

b + 2R := k1, known (1)

c + 2R := k2, known (2)

m(b + c)= ad (3)(by Ptolemy Theorem in the cyclic quadrilateral ABDC)

The triangle BCD has known angles (DCB = DBC = A/2, CDB = 180 - A)

==> a/m := t is known.

==> b + c = (a/m)d = td

ae + cn = bn (4)(by Ptolemy Theorem in the cyclic quadrilateral ABCE) ==>
e = (b - c)n/a

We have:

b - c = k1 - k2, known

n/a is known since the triangle CEB has known angles (CEB = A, ECB = EBC = 90 - (A/2))

Therefore e = (b - c)n/a is known.

EA^2 = AD^2 - AD^2 (5)(by Pythagorean Theorem in the right triangle ADE)or e^2 = 4R^2 - d^2, known.

Now, from:

(1) and (2) ==> b + c = k1 + k2 - 4R (6)

(6) and (3) ==> d = (k1 + k2 - 4R) / t (7)

(7) and (5) ==> 4R^2 - ((k1 + k2 - 4R)/t)^2 = e^2

== > R is known.

So the problem is equivalent to construct triangle if are given A, b - c, R or A, b - c, a (the solution is left to the reader).

Exercises:

To construct triangle ABC if are given:

1. A, h_b - a, h_c + a

2. A, h_b - a, h_c - a

TRIANGLE CONSTRUCTION A, 2b+a, 2c+a

To construct triangle ABC if are given A, 2b + a = m, 2c + a = n

Analysis

Let ABC be the triangle in question.

We have:

m+n = 2(a+b+c) = 4s ==> the semiperimeter s is known

m-n = 2(b-c) ==> the difference b-c is known

Let E,D the points the a-excircle (Ia) touches AC,BC, resp.
The triangle DAIa has:
ADIa = 90 d., DAIa = A/2, AD = s. Therefore IaD = IaE = r_b is known.

Let M be the midpoint of BC. We have BIaC = 90-(A/2) and ME = (|b-c|)/2.(So the problem is eqivalent to construct triangle if are given:
A, b-c, r_b)

IaM^2 = IaE^2 + ME^2 = (r_b)^2 + ((b-c)/2)^2 ==> the median IaM is known.

In the triangle IaBC we know the angle Ia, the altitude and the median from Ia, therefore the problem is equivalent to construct triangle if are given:

A, h_a, m_a (altitude, median from A, resp.). This construction is left to the reader.

Exercises:

To construct triangle ABC if are given:

1. A, 2b - a = m, 2c + a = n

2. A, 2b - a = m, 2c - a = n

TRIANGLE CONSTRUCTION A, a + b, a + c

To construct triangle ABC if are given A, a + b, a + c

Solution 1.

Analysis:

Let ABC be the triangle in question. Let D, E be two points on the extensions of AC,AB, resp. such that CD = BE = BC = a.

The parallel from A to BC intersects DB at Z.

The triangle AZB is similar to triangle CDB ==>

AZ / AD = CB / CD = 1 ==> AZ = AD (1)

The parallel from Z to AE intersects DE at Q.

The triangles AZQ and CBE are similar ==>

AZ / ZQ = CB / BE = 1 ==> ZQ = AZ (2)

(1) /\ (2) ==> AD = AZ = ZQ (3).

The parallel from Z to EQ intersects AB at H.

We have HE = ZQ (4) (since EHZQ is parallelogram)

(3) /\ (4) ==> HE = AD.

Construction:

I construct the triangle ADE such that AD = b+a, AE = c+a, angle DAE = A.

Let H be on AE such that EH = AD.

The circle (A, AD) intersects the parallel from H to DE at Z.

The line DZ intersects AE at B. The parallel from B to AZ intersects AD at C.

ABC is the required triangle.

The Proof and Investigation are left to the reader.

Reference:
Ioannis Panakis: Solutions of the Exercises of the MATHEMATICS of the 5th Class of Greek Gymnasium, vol I, Athens, Kokotsakis Bookstore, p. 90.

Solution 2.

Analysis:

Let ABC be the triangle in question. Let B', C' be two points on the extensions of AB,AC, resp. such that BB' = CC' = BC = a.

Let D be the intersection of the lines: Parallel from B' to BC and Parallel from C to BB'. The quadrilateral BCDB' is rhombus. The isosceles triangle DCC' has fixed angles: DCC' = A, CDC' = CC'D = (90-A)/2 ("remains similar to itself"). Therefore CD/C'D is fixed, and since CD = B'D ==> B'D/C'D is fixed.

So the point D lies on a known line forming with AC' angle (90-A)/2 and on the Apollonius circle (B'C', B'D/C'D).

The Construction, Proof and Investigation are left to the reader.

Reference:
EUCLID [publ. by the Greek Mathematical Society], December 1982.

Solution 3.

Analysis:

Let ABC be the triangle in question. Let B', C' be two points on the extensions of AB,AC, resp. such that BB' = CC' = BC = a.

Let D be the intersection of BC' and CB' and E the intersection of the parallel from C' to AB' and the parallel from B' to BC'.

The isosceles trianle CC'E has fixed angles:

(CC'E) = 180 - A, (C'CE) = (C'EC) = A/2.

We have:

Angle (CB'E) = (CDC') = (CBD) + (BCD) = C/2 + B/2 = 90 - (A/2) : fixed.

Construction:

I construct the triangle AB'C' such that AB' = c+a, AC' = b+a, angle (B'AC') = A. Let L be an arbitrary point on C'A and M a point on the parallel through C' to AB' such that C'L = C'M. The circle (LM, 90-(A/2)), ie the circle with chord LM and angle 90-(A/2), intersects B'C at N. The parallel through B' to LN intersects AC' at C. The parallel through B' to MN intersects C'M at E. The parallel through C' to B'E intersects AB' at B. The triangle ABC is the required triangle.

Proof (to prove B'B = BC = CC') / Investigation: Left to the reader.

Reference: A. P. Hatzipolakis (1982)

Exercise:
Contruct the triangle if are given:
1. A, b + a, c - a
2. A, b - a, c - a

TRIANGLE RESOLUTION A, a+b-c, R+r

Problem:
To resolve triangle ABC if are given A, a+b-c, R+r
See Hyacinthos Message #19749

Resolution:

We have:

sinA + sinB - sinC = 4sin(A/2)sin(B/2)cos(C/2)

r = 4Rsin(A/2)sin(B/2)sin(C/2)

==>

a+b-c = 2R(sinA+sinB-sinC) = 8Rsin(A/2)sin(B/2)cos(C/2)

R+r = R(1+4sin(A/2)sin(B/2)sin(C/2))

==>

t := (R+r)/(a+b-c) =

= (1+4sin(A/2)sin(B/2)sin(C/2))/8sin(A/2)sin(B/2)cos(C/2)

==>

4sin(A/2)sin(B/2)[sin(C/2) - 2tcos(C/2)] + 1 = 0

and since sin(B/2) = sin(90 - ((C+A)/2)) = cos((C+A)/2) =

= cos(C/2)cos(A/2) - sin(C/2)sin(A/2), ==>

4sin(A/2)[cos(A/2) + 2tsin(A/2)]sin(C/2)cos(C/2) - 4(sin(A/2)^2(sin(C/2))^2 - 8tsin(A/2)cos(A/2)(cos(A/2)^2 + 1 = 0.

We have the system of equations:

fx^2 + gy^2 + hxy + 1 = 0

x^2 + y^2 = 1

where x, y stand for the unknown sin(C/2),cos(C/2) and f,g,h are known coefficients. From these equations we get the equation:

Lx^4 + Mx^2 + N = 0, where L,M,N are known coefficients.

This equation has constructible roots [Read THIS], therefore the problem has a constructible Euclidean solution (ie by ruler and compass)

A CONFIGURATION (Case 3)

See THIS

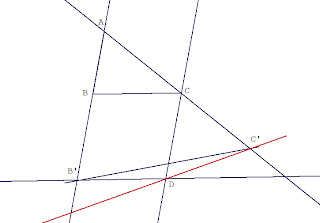
Let ABC be a triangle and P a point.

The circle (B, BP) intersects AB at Ac1 (between A,B) and Ac2 (on the extension of BA) AND BC at A1c (between B,C) and A2c (on the extension of BC). The circle (C, CP) intersects AC at Ab1 (between A,C) and Ab2 AND BC at A1b (between B,C) and A2b (on the extension of CB).

3. The lines Ab1A1b and Ac1A1c intersect at A3.

Which is the locus of P such that ABC, A3B3C3 are perspective?

Solution
by Francisco Javier García Capitán

The locus looks like Neuberg cubic + three circle arcs:

This is Neuberg Cubic:

Neuberg cubic in dotted line with the locus, showing that they are not exactly the same, but very very close:

The "circle arcs":

The algebraic curve of the eight degree of which the arcs are part, that is they are not really circle arcs:

Equations:

1. The Neuberg-like curve is part of a curve of degree 14 with 20178 terms

2. The equation of the octic (in barycentrics):

64 a^6 b^4 c^8 x^6 y^2 + 256 a^5 b^5 c^8 x^6 y^2 -
128 a^4 b^6 c^8 x^6 y^2 - 256 a^3 b^7 c^8 x^6 y^2 +
64 a^2 b^8 c^8 x^6 y^2 + 256 a^4 b^5 c^9 x^6 y^2 +
512 a^3 b^6 c^9 x^6 y^2 - 256 a^2 b^7 c^9 x^6 y^2 -
128 a^4 b^4 c^10 x^6 y^2 - 256 a^3 b^5 c^10 x^6 y^2 +
384 a^2 b^6 c^10 x^6 y^2 - 256 a^2 b^5 c^11 x^6 y^2 +
64 a^2 b^4 c^12 x^6 y^2 - 16 a^8 b^2 c^8 x^5 y^3 -
112 a^7 b^3 c^8 x^5 y^3 - 48 a^6 b^4 c^8 x^5 y^3 +
1136 a^5 b^5 c^8 x^5 y^3 - 496 a^4 b^6 c^8 x^5 y^3 -
528 a^3 b^7 c^8 x^5 y^3 + 48 a^2 b^8 c^8 x^5 y^3 +
16 a b^9 c^8 x^5 y^3 + 48 a^7 b^2 c^9 x^5 y^3 +
256 a^6 b^3 c^9 x^5 y^3 + 208 a^5 b^4 c^9 x^5 y^3 +
768 a^4 b^5 c^9 x^5 y^3 + 1104 a^3 b^6 c^9 x^5 y^3 -
256 a^2 b^7 c^9 x^5 y^3 - 80 a b^8 c^9 x^5 y^3 -
16 a^6 b^2 c^10 x^5 y^3 + 16 a^5 b^3 c^10 x^5 y^3 +
32 a^4 b^4 c^10 x^5 y^3 - 416 a^3 b^5 c^10 x^5 y^3 +
496 a^2 b^6 c^10 x^5 y^3 + 144 a b^7 c^10 x^5 y^3 -
80 a^5 b^2 c^11 x^5 y^3 - 384 a^4 b^3 c^11 x^5 y^3 -
352 a^3 b^4 c^11 x^5 y^3 - 384 a^2 b^5 c^11 x^5 y^3 -
80 a b^6 c^11 x^5 y^3 + 80 a^4 b^2 c^12 x^5 y^3 +
176 a^3 b^3 c^12 x^5 y^3 + 16 a^2 b^4 c^12 x^5 y^3 -
80 a b^5 c^12 x^5 y^3 + 16 a^3 b^2 c^13 x^5 y^3 +
128 a^2 b^3 c^13 x^5 y^3 + 144 a b^4 c^13 x^5 y^3 -
48 a^2 b^2 c^14 x^5 y^3 - 80 a b^3 c^14 x^5 y^3 +
16 a b^2 c^15 x^5 y^3 + a^10 c^8 x^4 y^4 + 10 a^9 b c^8 x^4 y^4 -
19 a^8 b^2 c^8 x^4 y^4 - 392 a^7 b^3 c^8 x^4 y^4 -
494 a^6 b^4 c^8 x^4 y^4 + 1788 a^5 b^5 c^8 x^4 y^4 -
494 a^4 b^6 c^8 x^4 y^4 - 392 a^3 b^7 c^8 x^4 y^4 -
19 a^2 b^8 c^8 x^4 y^4 + 10 a b^9 c^8 x^4 y^4 + b^10 c^8 x^4 y^4 -
6 a^9 c^9 x^4 y^4 - 54 a^8 b c^9 x^4 y^4 + 8 a^7 b^2 c^9 x^4 y^4 +
872 a^6 b^3 c^9 x^4 y^4 + 716 a^5 b^4 c^9 x^4 y^4 +
716 a^4 b^5 c^9 x^4 y^4 + 872 a^3 b^6 c^9 x^4 y^4 +
8 a^2 b^7 c^9 x^4 y^4 - 54 a b^8 c^9 x^4 y^4 - 6 b^9 c^9 x^4 y^4 +
13 a^8 c^10 x^4 y^4 + 104 a^7 b c^10 x^4 y^4 +
140 a^6 b^2 c^10 x^4 y^4 - 168 a^5 b^3 c^10 x^4 y^4 +
334 a^4 b^4 c^10 x^4 y^4 - 168 a^3 b^5 c^10 x^4 y^4 +
140 a^2 b^6 c^10 x^4 y^4 + 104 a b^7 c^10 x^4 y^4 +
13 b^8 c^10 x^4 y^4 - 8 a^7 c^11 x^4 y^4 - 56 a^6 b c^11 x^4 y^4 -
232 a^5 b^2 c^11 x^4 y^4 - 728 a^4 b^3 c^11 x^4 y^4 -
728 a^3 b^4 c^11 x^4 y^4 - 232 a^2 b^5 c^11 x^4 y^4 -
56 a b^6 c^11 x^4 y^4 - 8 b^7 c^11 x^4 y^4 - 14 a^6 c^12 x^4 y^4 -
84 a^5 b c^12 x^4 y^4 + 46 a^4 b^2 c^12 x^4 y^4 +
360 a^3 b^3 c^12 x^4 y^4 + 46 a^2 b^4 c^12 x^4 y^4 -
84 a b^5 c^12 x^4 y^4 - 14 b^6 c^12 x^4 y^4 + 28 a^5 c^13 x^4 y^4 +
140 a^4 b c^13 x^4 y^4 + 120 a^3 b^2 c^13 x^4 y^4 +
120 a^2 b^3 c^13 x^4 y^4 + 140 a b^4 c^13 x^4 y^4 +
28 b^5 c^13 x^4 y^4 - 14 a^4 c^14 x^4 y^4 - 56 a^3 b c^14 x^4 y^4 -
52 a^2 b^2 c^14 x^4 y^4 - 56 a b^3 c^14 x^4 y^4 -
14 b^4 c^14 x^4 y^4 - 8 a^3 c^15 x^4 y^4 - 24 a^2 b c^15 x^4 y^4 -
24 a b^2 c^15 x^4 y^4 - 8 b^3 c^15 x^4 y^4 + 13 a^2 c^16 x^4 y^4 +
26 a b c^16 x^4 y^4 + 13 b^2 c^16 x^4 y^4 - 6 a c^17 x^4 y^4 -
6 b c^17 x^4 y^4 + c^18 x^4 y^4 + 16 a^9 b c^8 x^3 y^5 +
48 a^8 b^2 c^8 x^3 y^5 - 528 a^7 b^3 c^8 x^3 y^5 -
496 a^6 b^4 c^8 x^3 y^5 + 1136 a^5 b^5 c^8 x^3 y^5 -
48 a^4 b^6 c^8 x^3 y^5 - 112 a^3 b^7 c^8 x^3 y^5 -
16 a^2 b^8 c^8 x^3 y^5 - 80 a^8 b c^9 x^3 y^5 -
256 a^7 b^2 c^9 x^3 y^5 + 1104 a^6 b^3 c^9 x^3 y^5 +
768 a^5 b^4 c^9 x^3 y^5 + 208 a^4 b^5 c^9 x^3 y^5 +
256 a^3 b^6 c^9 x^3 y^5 + 48 a^2 b^7 c^9 x^3 y^5 +
144 a^7 b c^10 x^3 y^5 + 496 a^6 b^2 c^10 x^3 y^5 -
416 a^5 b^3 c^10 x^3 y^5 + 32 a^4 b^4 c^10 x^3 y^5 +
16 a^3 b^5 c^10 x^3 y^5 - 16 a^2 b^6 c^10 x^3 y^5 -
80 a^6 b c^11 x^3 y^5 - 384 a^5 b^2 c^11 x^3 y^5 -
352 a^4 b^3 c^11 x^3 y^5 - 384 a^3 b^4 c^11 x^3 y^5 -
80 a^2 b^5 c^11 x^3 y^5 - 80 a^5 b c^12 x^3 y^5 +
16 a^4 b^2 c^12 x^3 y^5 + 176 a^3 b^3 c^12 x^3 y^5 +
80 a^2 b^4 c^12 x^3 y^5 + 144 a^4 b c^13 x^3 y^5 +
128 a^3 b^2 c^13 x^3 y^5 + 16 a^2 b^3 c^13 x^3 y^5 -
80 a^3 b c^14 x^3 y^5 - 48 a^2 b^2 c^14 x^3 y^5 +
16 a^2 b c^15 x^3 y^5 + 64 a^8 b^2 c^8 x^2 y^6 -
256 a^7 b^3 c^8 x^2 y^6 - 128 a^6 b^4 c^8 x^2 y^6 +
256 a^5 b^5 c^8 x^2 y^6 + 64 a^4 b^6 c^8 x^2 y^6 -
256 a^7 b^2 c^9 x^2 y^6 + 512 a^6 b^3 c^9 x^2 y^6 +
256 a^5 b^4 c^9 x^2 y^6 + 384 a^6 b^2 c^10 x^2 y^6 -
256 a^5 b^3 c^10 x^2 y^6 - 128 a^4 b^4 c^10 x^2 y^6 -
256 a^5 b^2 c^11 x^2 y^6 + 64 a^4 b^2 c^12 x^2 y^6 +
384 a^6 b^6 c^6 x^6 y z + 256 a^5 b^7 c^6 x^6 y z -
512 a^4 b^8 c^6 x^6 y z - 256 a^3 b^9 c^6 x^6 y z +
128 a^2 b^10 c^6 x^6 y z + 256 a^5 b^6 c^7 x^6 y z +
1024 a^4 b^7 c^7 x^6 y z + 256 a^3 b^8 c^7 x^6 y z -
512 a^2 b^9 c^7 x^6 y z - 512 a^4 b^6 c^8 x^6 y z +
256 a^3 b^7 c^8 x^6 y z + 768 a^2 b^8 c^8 x^6 y z -
256 a^3 b^6 c^9 x^6 y z - 512 a^2 b^7 c^9 x^6 y z +
128 a^2 b^6 c^10 x^6 y z + 80 a^8 b^4 c^6 x^5 y^2 z -
176 a^7 b^5 c^6 x^5 y^2 z + 1424 a^6 b^6 c^6 x^5 y^2 z +
400 a^5 b^7 c^6 x^5 y^2 z - 1552 a^4 b^8 c^6 x^5 y^2 z -
272 a^3 b^9 c^6 x^5 y^2 z + 48 a^2 b^10 c^6 x^5 y^2 z +
48 a b^11 c^6 x^5 y^2 z + 240 a^7 b^4 c^7 x^5 y^2 z +
768 a^6 b^5 c^7 x^5 y^2 z + 2480 a^5 b^6 c^7 x^5 y^2 z +
2176 a^4 b^7 c^7 x^5 y^2 z + 80 a^3 b^8 c^7 x^5 y^2 z -
384 a^2 b^9 c^7 x^5 y^2 z - 240 a b^10 c^7 x^5 y^2 z -
80 a^6 b^4 c^8 x^5 y^2 z + 1520 a^5 b^5 c^8 x^5 y^2 z +
352 a^4 b^6 c^8 x^5 y^2 z + 352 a^3 b^7 c^8 x^5 y^2 z +
1008 a^2 b^8 c^8 x^5 y^2 z + 432 a b^9 c^8 x^5 y^2 z -
560 a^5 b^4 c^9 x^5 y^2 z - 1024 a^4 b^5 c^9 x^5 y^2 z +
416 a^3 b^6 c^9 x^5 y^2 z - 1152 a^2 b^7 c^9 x^5 y^2 z -
240 a b^8 c^9 x^5 y^2 z + 48 a^4 b^4 c^10 x^5 y^2 z -
848 a^3 b^5 c^10 x^5 y^2 z + 528 a^2 b^6 c^10 x^5 y^2 z -
240 a b^7 c^10 x^5 y^2 z + 272 a^3 b^4 c^11 x^5 y^2 z +
432 a b^6 c^11 x^5 y^2 z - 48 a^2 b^4 c^12 x^5 y^2 z -
240 a b^5 c^12 x^5 y^2 z + 48 a b^4 c^13 x^5 y^2 z -
12 a^10 b^2 c^6 x^4 y^3 z - 24 a^9 b^3 c^6 x^4 y^3 z -
316 a^8 b^4 c^6 x^4 y^3 z - 208 a^7 b^5 c^6 x^4 y^3 z +
1912 a^6 b^6 c^6 x^4 y^3 z + 256 a^5 b^7 c^6 x^4 y^3 z -
1544 a^4 b^8 c^6 x^4 y^3 z - 48 a^3 b^9 c^6 x^4 y^3 z -
44 a^2 b^10 c^6 x^4 y^3 z + 24 a b^11 c^6 x^4 y^3 z +
4 b^12 c^6 x^4 y^3 z + 8 a^9 b^2 c^7 x^4 y^3 z -
120 a^8 b^3 c^7 x^4 y^3 z + 1072 a^7 b^4 c^7 x^4 y^3 z +
3136 a^6 b^5 c^7 x^4 y^3 z + 4480 a^5 b^6 c^7 x^4 y^3 z +
2128 a^4 b^7 c^7 x^4 y^3 z - 304 a^3 b^8 c^7 x^4 y^3 z -
136 a b^10 c^7 x^4 y^3 z - 24 b^11 c^7 x^4 y^3 z +
68 a^8 b^2 c^8 x^4 y^3 z + 368 a^7 b^3 c^8 x^4 y^3 z +
144 a^6 b^4 c^8 x^4 y^3 z + 5376 a^5 b^5 c^8 x^4 y^3 z +
904 a^4 b^6 c^8 x^4 y^3 z + 624 a^3 b^7 c^8 x^4 y^3 z +
368 a^2 b^8 c^8 x^4 y^3 z + 288 a b^9 c^8 x^4 y^3 z +
52 b^10 c^8 x^4 y^3 z - 80 a^7 b^2 c^9 x^4 y^3 z -
1536 a^5 b^4 c^9 x^4 y^3 z - 1824 a^4 b^5 c^9 x^4 y^3 z +
432 a^3 b^6 c^9 x^4 y^3 z - 576 a^2 b^7 c^9 x^4 y^3 z -
224 a b^8 c^9 x^4 y^3 z - 32 b^9 c^9 x^4 y^3 z -
72 a^6 b^2 c^10 x^4 y^3 z - 512 a^5 b^3 c^10 x^4 y^3 z +
136 a^4 b^4 c^10 x^4 y^3 z - 1232 a^3 b^5 c^10 x^4 y^3 z +
184 a^2 b^6 c^10 x^4 y^3 z - 112 a b^7 c^10 x^4 y^3 z -
56 b^8 c^10 x^4 y^3 z + 128 a^5 b^2 c^11 x^4 y^3 z +
208 a^4 b^3 c^11 x^4 y^3 z + 432 a^3 b^4 c^11 x^4 y^3 z +
128 a^2 b^5 c^11 x^4 y^3 z + 336 a b^6 c^11 x^4 y^3 z +
112 b^7 c^11 x^4 y^3 z - 8 a^4 b^2 c^12 x^4 y^3 z +
144 a^3 b^3 c^12 x^4 y^3 z - 16 a^2 b^4 c^12 x^4 y^3 z -
224 a b^5 c^12 x^4 y^3 z - 56 b^6 c^12 x^4 y^3 z -
48 a^3 b^2 c^13 x^4 y^3 z - 64 a^2 b^3 c^13 x^4 y^3 z +
32 a b^4 c^13 x^4 y^3 z - 32 b^5 c^13 x^4 y^3 z +
20 a^2 b^2 c^14 x^4 y^3 z + 24 a b^3 c^14 x^4 y^3 z +
52 b^4 c^14 x^4 y^3 z - 8 a b^2 c^15 x^4 y^3 z -
24 b^3 c^15 x^4 y^3 z + 4 b^2 c^16 x^4 y^3 z +
4 a^12 c^6 x^3 y^4 z + 24 a^11 b c^6 x^3 y^4 z -
44 a^10 b^2 c^6 x^3 y^4 z - 48 a^9 b^3 c^6 x^3 y^4 z -
1544 a^8 b^4 c^6 x^3 y^4 z + 256 a^7 b^5 c^6 x^3 y^4 z +
1912 a^6 b^6 c^6 x^3 y^4 z - 208 a^5 b^7 c^6 x^3 y^4 z -
316 a^4 b^8 c^6 x^3 y^4 z - 24 a^3 b^9 c^6 x^3 y^4 z -
12 a^2 b^10 c^6 x^3 y^4 z - 24 a^11 c^7 x^3 y^4 z -
136 a^10 b c^7 x^3 y^4 z - 304 a^8 b^3 c^7 x^3 y^4 z +
2128 a^7 b^4 c^7 x^3 y^4 z + 4480 a^6 b^5 c^7 x^3 y^4 z +
3136 a^5 b^6 c^7 x^3 y^4 z + 1072 a^4 b^7 c^7 x^3 y^4 z -
120 a^3 b^8 c^7 x^3 y^4 z + 8 a^2 b^9 c^7 x^3 y^4 z +
52 a^10 c^8 x^3 y^4 z + 288 a^9 b c^8 x^3 y^4 z +
368 a^8 b^2 c^8 x^3 y^4 z + 624 a^7 b^3 c^8 x^3 y^4 z +
904 a^6 b^4 c^8 x^3 y^4 z + 5376 a^5 b^5 c^8 x^3 y^4 z +
144 a^4 b^6 c^8 x^3 y^4 z + 368 a^3 b^7 c^8 x^3 y^4 z +
68 a^2 b^8 c^8 x^3 y^4 z - 32 a^9 c^9 x^3 y^4 z -
224 a^8 b c^9 x^3 y^4 z - 576 a^7 b^2 c^9 x^3 y^4 z +
432 a^6 b^3 c^9 x^3 y^4 z - 1824 a^5 b^4 c^9 x^3 y^4 z -
1536 a^4 b^5 c^9 x^3 y^4 z - 80 a^2 b^7 c^9 x^3 y^4 z -
56 a^8 c^10 x^3 y^4 z - 112 a^7 b c^10 x^3 y^4 z +
184 a^6 b^2 c^10 x^3 y^4 z - 1232 a^5 b^3 c^10 x^3 y^4 z +
136 a^4 b^4 c^10 x^3 y^4 z - 512 a^3 b^5 c^10 x^3 y^4 z -
72 a^2 b^6 c^10 x^3 y^4 z + 112 a^7 c^11 x^3 y^4 z +
336 a^6 b c^11 x^3 y^4 z + 128 a^5 b^2 c^11 x^3 y^4 z +
432 a^4 b^3 c^11 x^3 y^4 z + 208 a^3 b^4 c^11 x^3 y^4 z +
128 a^2 b^5 c^11 x^3 y^4 z - 56 a^6 c^12 x^3 y^4 z -
224 a^5 b c^12 x^3 y^4 z - 16 a^4 b^2 c^12 x^3 y^4 z +
144 a^3 b^3 c^12 x^3 y^4 z - 8 a^2 b^4 c^12 x^3 y^4 z -
32 a^5 c^13 x^3 y^4 z + 32 a^4 b c^13 x^3 y^4 z -
64 a^3 b^2 c^13 x^3 y^4 z - 48 a^2 b^3 c^13 x^3 y^4 z +
52 a^4 c^14 x^3 y^4 z + 24 a^3 b c^14 x^3 y^4 z +
20 a^2 b^2 c^14 x^3 y^4 z - 24 a^3 c^15 x^3 y^4 z -
8 a^2 b c^15 x^3 y^4 z + 4 a^2 c^16 x^3 y^4 z +
48 a^11 b c^6 x^2 y^5 z + 48 a^10 b^2 c^6 x^2 y^5 z -
272 a^9 b^3 c^6 x^2 y^5 z - 1552 a^8 b^4 c^6 x^2 y^5 z +
400 a^7 b^5 c^6 x^2 y^5 z + 1424 a^6 b^6 c^6 x^2 y^5 z -
176 a^5 b^7 c^6 x^2 y^5 z + 80 a^4 b^8 c^6 x^2 y^5 z -
240 a^10 b c^7 x^2 y^5 z - 384 a^9 b^2 c^7 x^2 y^5 z +
80 a^8 b^3 c^7 x^2 y^5 z + 2176 a^7 b^4 c^7 x^2 y^5 z +
2480 a^6 b^5 c^7 x^2 y^5 z + 768 a^5 b^6 c^7 x^2 y^5 z +
240 a^4 b^7 c^7 x^2 y^5 z + 432 a^9 b c^8 x^2 y^5 z +
1008 a^8 b^2 c^8 x^2 y^5 z + 352 a^7 b^3 c^8 x^2 y^5 z +
352 a^6 b^4 c^8 x^2 y^5 z + 1520 a^5 b^5 c^8 x^2 y^5 z -
80 a^4 b^6 c^8 x^2 y^5 z - 240 a^8 b c^9 x^2 y^5 z -
1152 a^7 b^2 c^9 x^2 y^5 z + 416 a^6 b^3 c^9 x^2 y^5 z -
1024 a^5 b^4 c^9 x^2 y^5 z - 560 a^4 b^5 c^9 x^2 y^5 z -
240 a^7 b c^10 x^2 y^5 z + 528 a^6 b^2 c^10 x^2 y^5 z -
848 a^5 b^3 c^10 x^2 y^5 z + 48 a^4 b^4 c^10 x^2 y^5 z +
432 a^6 b c^11 x^2 y^5 z + 272 a^4 b^3 c^11 x^2 y^5 z -
240 a^5 b c^12 x^2 y^5 z - 48 a^4 b^2 c^12 x^2 y^5 z +
48 a^4 b c^13 x^2 y^5 z + 128 a^10 b^2 c^6 x y^6 z -
256 a^9 b^3 c^6 x y^6 z - 512 a^8 b^4 c^6 x y^6 z +
256 a^7 b^5 c^6 x y^6 z + 384 a^6 b^6 c^6 x y^6 z -
512 a^9 b^2 c^7 x y^6 z + 256 a^8 b^3 c^7 x y^6 z +
1024 a^7 b^4 c^7 x y^6 z + 256 a^6 b^5 c^7 x y^6 z +
768 a^8 b^2 c^8 x y^6 z + 256 a^7 b^3 c^8 x y^6 z -
512 a^6 b^4 c^8 x y^6 z - 512 a^7 b^2 c^9 x y^6 z -
256 a^6 b^3 c^9 x y^6 z + 128 a^6 b^2 c^10 x y^6 z +
64 a^6 b^8 c^4 x^6 z^2 - 128 a^4 b^10 c^4 x^6 z^2 +
64 a^2 b^12 c^4 x^6 z^2 + 256 a^5 b^8 c^5 x^6 z^2 +
256 a^4 b^9 c^5 x^6 z^2 - 256 a^3 b^10 c^5 x^6 z^2 -
256 a^2 b^11 c^5 x^6 z^2 - 128 a^4 b^8 c^6 x^6 z^2 +
512 a^3 b^9 c^6 x^6 z^2 + 384 a^2 b^10 c^6 x^6 z^2 -
256 a^3 b^8 c^7 x^6 z^2 - 256 a^2 b^9 c^7 x^6 z^2 +
64 a^2 b^8 c^8 x^6 z^2 + 80 a^8 b^6 c^4 x^5 y z^2 +
240 a^7 b^7 c^4 x^5 y z^2 - 80 a^6 b^8 c^4 x^5 y z^2 -
560 a^5 b^9 c^4 x^5 y z^2 + 48 a^4 b^10 c^4 x^5 y z^2 +
272 a^3 b^11 c^4 x^5 y z^2 - 48 a^2 b^12 c^4 x^5 y z^2 +
48 a b^13 c^4 x^5 y z^2 - 176 a^7 b^6 c^5 x^5 y z^2 +
768 a^6 b^7 c^5 x^5 y z^2 + 1520 a^5 b^8 c^5 x^5 y z^2 -
1024 a^4 b^9 c^5 x^5 y z^2 - 848 a^3 b^10 c^5 x^5 y z^2 -
240 a b^12 c^5 x^5 y z^2 + 1424 a^6 b^6 c^6 x^5 y z^2 +
2480 a^5 b^7 c^6 x^5 y z^2 + 352 a^4 b^8 c^6 x^5 y z^2 +
416 a^3 b^9 c^6 x^5 y z^2 + 528 a^2 b^10 c^6 x^5 y z^2 +
432 a b^11 c^6 x^5 y z^2 + 400 a^5 b^6 c^7 x^5 y z^2 +
2176 a^4 b^7 c^7 x^5 y z^2 + 352 a^3 b^8 c^7 x^5 y z^2 -
1152 a^2 b^9 c^7 x^5 y z^2 - 240 a b^10 c^7 x^5 y z^2 -
1552 a^4 b^6 c^8 x^5 y z^2 + 80 a^3 b^7 c^8 x^5 y z^2 +
1008 a^2 b^8 c^8 x^5 y z^2 - 240 a b^9 c^8 x^5 y z^2 -
272 a^3 b^6 c^9 x^5 y z^2 - 384 a^2 b^7 c^9 x^5 y z^2 +
432 a b^8 c^9 x^5 y z^2 + 48 a^2 b^6 c^10 x^5 y z^2 -
240 a b^7 c^10 x^5 y z^2 + 48 a b^6 c^11 x^5 y z^2 +
294 a^10 b^4 c^4 x^4 y^2 z^2 - 276 a^9 b^5 c^4 x^4 y^2 z^2 +
142 a^8 b^6 c^4 x^4 y^2 z^2 + 624 a^7 b^7 c^4 x^4 y^2 z^2 -
916 a^6 b^8 c^4 x^4 y^2 z^2 - 664 a^5 b^9 c^4 x^4 y^2 z^2 +
492 a^4 b^10 c^4 x^4 y^2 z^2 + 304 a^3 b^11 c^4 x^4 y^2 z^2 -
18 a^2 b^12 c^4 x^4 y^2 z^2 + 12 a b^13 c^4 x^4 y^2 z^2 +
6 b^14 c^4 x^4 y^2 z^2 - 276 a^9 b^4 c^5 x^4 y^2 z^2 -
388 a^8 b^5 c^5 x^4 y^2 z^2 + 816 a^7 b^6 c^5 x^4 y^2 z^2 +
1552 a^6 b^7 c^5 x^4 y^2 z^2 + 1032 a^5 b^8 c^5 x^4 y^2 z^2 -
1592 a^4 b^9 c^5 x^4 y^2 z^2 - 976 a^3 b^10 c^5 x^4 y^2 z^2 -
48 a^2 b^11 c^5 x^4 y^2 z^2 - 84 a b^12 c^5 x^4 y^2 z^2 -
36 b^13 c^5 x^4 y^2 z^2 + 142 a^8 b^4 c^6 x^4 y^2 z^2 +
816 a^7 b^5 c^6 x^4 y^2 z^2 + 8072 a^6 b^6 c^6 x^4 y^2 z^2 +
5776 a^5 b^7 c^6 x^4 y^2 z^2 - 876 a^4 b^8 c^6 x^4 y^2 z^2 +
1104 a^3 b^9 c^6 x^4 y^2 z^2 + 264 a^2 b^10 c^6 x^4 y^2 z^2 +
240 a b^11 c^6 x^4 y^2 z^2 + 78 b^12 c^6 x^4 y^2 z^2 +
624 a^7 b^4 c^7 x^4 y^2 z^2 + 1552 a^6 b^5 c^7 x^4 y^2 z^2 +
5776 a^5 b^6 c^7 x^4 y^2 z^2 + 3952 a^4 b^7 c^7 x^4 y^2 z^2 -
432 a^3 b^8 c^7 x^4 y^2 z^2 - 336 a^2 b^9 c^7 x^4 y^2 z^2 -
336 a b^10 c^7 x^4 y^2 z^2 - 48 b^11 c^7 x^4 y^2 z^2 -
916 a^6 b^4 c^8 x^4 y^2 z^2 + 1032 a^5 b^5 c^8 x^4 y^2 z^2 -
876 a^4 b^6 c^8 x^4 y^2 z^2 - 432 a^3 b^7 c^8 x^4 y^2 z^2 +
276 a^2 b^8 c^8 x^4 y^2 z^2 + 168 a b^9 c^8 x^4 y^2 z^2 -
84 b^10 c^8 x^4 y^2 z^2 - 664 a^5 b^4 c^9 x^4 y^2 z^2 -
1592 a^4 b^5 c^9 x^4 y^2 z^2 + 1104 a^3 b^6 c^9 x^4 y^2 z^2 -
336 a^2 b^7 c^9 x^4 y^2 z^2 + 168 a b^8 c^9 x^4 y^2 z^2 +
168 b^9 c^9 x^4 y^2 z^2 + 492 a^4 b^4 c^10 x^4 y^2 z^2 -
976 a^3 b^5 c^10 x^4 y^2 z^2 + 264 a^2 b^6 c^10 x^4 y^2 z^2 -
336 a b^7 c^10 x^4 y^2 z^2 - 84 b^8 c^10 x^4 y^2 z^2 +
304 a^3 b^4 c^11 x^4 y^2 z^2 - 48 a^2 b^5 c^11 x^4 y^2 z^2 +
240 a b^6 c^11 x^4 y^2 z^2 - 48 b^7 c^11 x^4 y^2 z^2 -
18 a^2 b^4 c^12 x^4 y^2 z^2 - 84 a b^5 c^12 x^4 y^2 z^2 +
78 b^6 c^12 x^4 y^2 z^2 + 12 a b^4 c^13 x^4 y^2 z^2 -
36 b^5 c^13 x^4 y^2 z^2 + 6 b^4 c^14 x^4 y^2 z^2 +
28 a^12 b^2 c^4 x^3 y^3 z^2 + 8 a^11 b^3 c^4 x^3 y^3 z^2 +
844 a^10 b^4 c^4 x^3 y^3 z^2 - 608 a^9 b^5 c^4 x^3 y^3 z^2 -
872 a^8 b^6 c^4 x^3 y^3 z^2 + 1200 a^7 b^7 c^4 x^3 y^3 z^2 -
872 a^6 b^8 c^4 x^3 y^3 z^2 - 608 a^5 b^9 c^4 x^3 y^3 z^2 +
844 a^4 b^10 c^4 x^3 y^3 z^2 + 8 a^3 b^11 c^4 x^3 y^3 z^2 +
28 a^2 b^12 c^4 x^3 y^3 z^2 - 136 a^11 b^2 c^5 x^3 y^3 z^2 -
216 a^10 b^3 c^5 x^3 y^3 z^2 - 1008 a^9 b^4 c^5 x^3 y^3 z^2 -
464 a^8 b^5 c^5 x^3 y^3 z^2 + 1824 a^7 b^6 c^5 x^3 y^3 z^2 +
1824 a^6 b^7 c^5 x^3 y^3 z^2 - 464 a^5 b^8 c^5 x^3 y^3 z^2 -
1008 a^4 b^9 c^5 x^3 y^3 z^2 - 216 a^3 b^10 c^5 x^3 y^3 z^2 -
136 a^2 b^11 c^5 x^3 y^3 z^2 + 204 a^10 b^2 c^6 x^3 y^3 z^2 +
624 a^9 b^3 c^6 x^3 y^3 z^2 - 848 a^8 b^4 c^6 x^3 y^3 z^2 +
4496 a^7 b^5 c^6 x^3 y^3 z^2 + 12552 a^6 b^6 c^6 x^3 y^3 z^2 +
4496 a^5 b^7 c^6 x^3 y^3 z^2 - 848 a^4 b^8 c^6 x^3 y^3 z^2 +
624 a^3 b^9 c^6 x^3 y^3 z^2 + 204 a^2 b^10 c^6 x^3 y^3 z^2 -
592 a^8 b^3 c^7 x^3 y^3 z^2 + 2736 a^7 b^4 c^7 x^3 y^3 z^2 +
6560 a^6 b^5 c^7 x^3 y^3 z^2 + 6560 a^5 b^6 c^7 x^3 y^3 z^2 +
2736 a^4 b^7 c^7 x^3 y^3 z^2 - 592 a^3 b^8 c^7 x^3 y^3 z^2 -
296 a^8 b^2 c^8 x^3 y^3 z^2 - 64 a^7 b^3 c^8 x^3 y^3 z^2 -
1208 a^6 b^4 c^8 x^3 y^3 z^2 + 3008 a^5 b^5 c^8 x^3 y^3 z^2 -
1208 a^4 b^6 c^8 x^3 y^3 z^2 - 64 a^3 b^7 c^8 x^3 y^3 z^2 -
296 a^2 b^8 c^8 x^3 y^3 z^2 + 304 a^7 b^2 c^9 x^3 y^3 z^2 +
704 a^6 b^3 c^9 x^3 y^3 z^2 - 1936 a^5 b^4 c^9 x^3 y^3 z^2 -
1936 a^4 b^5 c^9 x^3 y^3 z^2 + 704 a^3 b^6 c^9 x^3 y^3 z^2 +
304 a^2 b^7 c^9 x^3 y^3 z^2 - 104 a^6 b^2 c^10 x^3 y^3 z^2 -
752 a^5 b^3 c^10 x^3 y^3 z^2 + 1072 a^4 b^4 c^10 x^3 y^3 z^2 -
752 a^3 b^5 c^10 x^3 y^3 z^2 - 104 a^2 b^6 c^10 x^3 y^3 z^2 -
64 a^5 b^2 c^11 x^3 y^3 z^2 + 208 a^4 b^3 c^11 x^3 y^3 z^2 +
208 a^3 b^4 c^11 x^3 y^3 z^2 - 64 a^2 b^5 c^11 x^3 y^3 z^2 +
140 a^4 b^2 c^12 x^3 y^3 z^2 + 184 a^3 b^3 c^12 x^3 y^3 z^2 +
140 a^2 b^4 c^12 x^3 y^3 z^2 - 104 a^3 b^2 c^13 x^3 y^3 z^2 -
104 a^2 b^3 c^13 x^3 y^3 z^2 + 28 a^2 b^2 c^14 x^3 y^3 z^2 +
6 a^14 c^4 x^2 y^4 z^2 + 12 a^13 b c^4 x^2 y^4 z^2 -
18 a^12 b^2 c^4 x^2 y^4 z^2 + 304 a^11 b^3 c^4 x^2 y^4 z^2 +
492 a^10 b^4 c^4 x^2 y^4 z^2 - 664 a^9 b^5 c^4 x^2 y^4 z^2 -
916 a^8 b^6 c^4 x^2 y^4 z^2 + 624 a^7 b^7 c^4 x^2 y^4 z^2 +
142 a^6 b^8 c^4 x^2 y^4 z^2 - 276 a^5 b^9 c^4 x^2 y^4 z^2 +
294 a^4 b^10 c^4 x^2 y^4 z^2 - 36 a^13 c^5 x^2 y^4 z^2 -
84 a^12 b c^5 x^2 y^4 z^2 - 48 a^11 b^2 c^5 x^2 y^4 z^2 -
976 a^10 b^3 c^5 x^2 y^4 z^2 - 1592 a^9 b^4 c^5 x^2 y^4 z^2 +
1032 a^8 b^5 c^5 x^2 y^4 z^2 + 1552 a^7 b^6 c^5 x^2 y^4 z^2 +
816 a^6 b^7 c^5 x^2 y^4 z^2 - 388 a^5 b^8 c^5 x^2 y^4 z^2 -
276 a^4 b^9 c^5 x^2 y^4 z^2 + 78 a^12 c^6 x^2 y^4 z^2 +
240 a^11 b c^6 x^2 y^4 z^2 + 264 a^10 b^2 c^6 x^2 y^4 z^2 +
1104 a^9 b^3 c^6 x^2 y^4 z^2 - 876 a^8 b^4 c^6 x^2 y^4 z^2 +
5776 a^7 b^5 c^6 x^2 y^4 z^2 + 8072 a^6 b^6 c^6 x^2 y^4 z^2 +
816 a^5 b^7 c^6 x^2 y^4 z^2 + 142 a^4 b^8 c^6 x^2 y^4 z^2 -
48 a^11 c^7 x^2 y^4 z^2 - 336 a^10 b c^7 x^2 y^4 z^2 -
336 a^9 b^2 c^7 x^2 y^4 z^2 - 432 a^8 b^3 c^7 x^2 y^4 z^2 +
3952 a^7 b^4 c^7 x^2 y^4 z^2 + 5776 a^6 b^5 c^7 x^2 y^4 z^2 +
1552 a^5 b^6 c^7 x^2 y^4 z^2 + 624 a^4 b^7 c^7 x^2 y^4 z^2 -
84 a^10 c^8 x^2 y^4 z^2 + 168 a^9 b c^8 x^2 y^4 z^2 +
276 a^8 b^2 c^8 x^2 y^4 z^2 - 432 a^7 b^3 c^8 x^2 y^4 z^2 -
876 a^6 b^4 c^8 x^2 y^4 z^2 + 1032 a^5 b^5 c^8 x^2 y^4 z^2 -
916 a^4 b^6 c^8 x^2 y^4 z^2 + 168 a^9 c^9 x^2 y^4 z^2 +
168 a^8 b c^9 x^2 y^4 z^2 - 336 a^7 b^2 c^9 x^2 y^4 z^2 +
1104 a^6 b^3 c^9 x^2 y^4 z^2 - 1592 a^5 b^4 c^9 x^2 y^4 z^2 -
664 a^4 b^5 c^9 x^2 y^4 z^2 - 84 a^8 c^10 x^2 y^4 z^2 -
336 a^7 b c^10 x^2 y^4 z^2 + 264 a^6 b^2 c^10 x^2 y^4 z^2 -
976 a^5 b^3 c^10 x^2 y^4 z^2 + 492 a^4 b^4 c^10 x^2 y^4 z^2 -
48 a^7 c^11 x^2 y^4 z^2 + 240 a^6 b c^11 x^2 y^4 z^2 -
48 a^5 b^2 c^11 x^2 y^4 z^2 + 304 a^4 b^3 c^11 x^2 y^4 z^2 +
78 a^6 c^12 x^2 y^4 z^2 - 84 a^5 b c^12 x^2 y^4 z^2 -
18 a^4 b^2 c^12 x^2 y^4 z^2 - 36 a^5 c^13 x^2 y^4 z^2 +
12 a^4 b c^13 x^2 y^4 z^2 + 6 a^4 c^14 x^2 y^4 z^2 +
48 a^13 b c^4 x y^5 z^2 - 48 a^12 b^2 c^4 x y^5 z^2 +
272 a^11 b^3 c^4 x y^5 z^2 + 48 a^10 b^4 c^4 x y^5 z^2 -
560 a^9 b^5 c^4 x y^5 z^2 - 80 a^8 b^6 c^4 x y^5 z^2 +
240 a^7 b^7 c^4 x y^5 z^2 + 80 a^6 b^8 c^4 x y^5 z^2 -
240 a^12 b c^5 x y^5 z^2 - 848 a^10 b^3 c^5 x y^5 z^2 -
1024 a^9 b^4 c^5 x y^5 z^2 + 1520 a^8 b^5 c^5 x y^5 z^2 +
768 a^7 b^6 c^5 x y^5 z^2 - 176 a^6 b^7 c^5 x y^5 z^2 +
432 a^11 b c^6 x y^5 z^2 + 528 a^10 b^2 c^6 x y^5 z^2 +
416 a^9 b^3 c^6 x y^5 z^2 + 352 a^8 b^4 c^6 x y^5 z^2 +
2480 a^7 b^5 c^6 x y^5 z^2 + 1424 a^6 b^6 c^6 x y^5 z^2 -
240 a^10 b c^7 x y^5 z^2 - 1152 a^9 b^2 c^7 x y^5 z^2 +
352 a^8 b^3 c^7 x y^5 z^2 + 2176 a^7 b^4 c^7 x y^5 z^2 +
400 a^6 b^5 c^7 x y^5 z^2 - 240 a^9 b c^8 x y^5 z^2 +
1008 a^8 b^2 c^8 x y^5 z^2 + 80 a^7 b^3 c^8 x y^5 z^2 -
1552 a^6 b^4 c^8 x y^5 z^2 + 432 a^8 b c^9 x y^5 z^2 -
384 a^7 b^2 c^9 x y^5 z^2 - 272 a^6 b^3 c^9 x y^5 z^2 -
240 a^7 b c^10 x y^5 z^2 + 48 a^6 b^2 c^10 x y^5 z^2 +
48 a^6 b c^11 x y^5 z^2 + 64 a^12 b^2 c^4 y^6 z^2 -
128 a^10 b^4 c^4 y^6 z^2 + 64 a^8 b^6 c^4 y^6 z^2 -
256 a^11 b^2 c^5 y^6 z^2 - 256 a^10 b^3 c^5 y^6 z^2 +
256 a^9 b^4 c^5 y^6 z^2 + 256 a^8 b^5 c^5 y^6 z^2 +
384 a^10 b^2 c^6 y^6 z^2 + 512 a^9 b^3 c^6 y^6 z^2 -
128 a^8 b^4 c^6 y^6 z^2 - 256 a^9 b^2 c^7 y^6 z^2 -
256 a^8 b^3 c^7 y^6 z^2 + 64 a^8 b^2 c^8 y^6 z^2 -
16 a^8 b^8 c^2 x^5 z^3 + 48 a^7 b^9 c^2 x^5 z^3 -
16 a^6 b^10 c^2 x^5 z^3 - 80 a^5 b^11 c^2 x^5 z^3 +
80 a^4 b^12 c^2 x^5 z^3 + 16 a^3 b^13 c^2 x^5 z^3 -
48 a^2 b^14 c^2 x^5 z^3 + 16 a b^15 c^2 x^5 z^3 -
112 a^7 b^8 c^3 x^5 z^3 + 256 a^6 b^9 c^3 x^5 z^3 +
16 a^5 b^10 c^3 x^5 z^3 - 384 a^4 b^11 c^3 x^5 z^3 +
176 a^3 b^12 c^3 x^5 z^3 + 128 a^2 b^13 c^3 x^5 z^3 -
80 a b^14 c^3 x^5 z^3 - 48 a^6 b^8 c^4 x^5 z^3 +
208 a^5 b^9 c^4 x^5 z^3 + 32 a^4 b^10 c^4 x^5 z^3 -
352 a^3 b^11 c^4 x^5 z^3 + 16 a^2 b^12 c^4 x^5 z^3 +
144 a b^13 c^4 x^5 z^3 + 1136 a^5 b^8 c^5 x^5 z^3 +
768 a^4 b^9 c^5 x^5 z^3 - 416 a^3 b^10 c^5 x^5 z^3 -
384 a^2 b^11 c^5 x^5 z^3 - 80 a b^12 c^5 x^5 z^3 -
496 a^4 b^8 c^6 x^5 z^3 + 1104 a^3 b^9 c^6 x^5 z^3 +
496 a^2 b^10 c^6 x^5 z^3 - 80 a b^11 c^6 x^5 z^3 -
528 a^3 b^8 c^7 x^5 z^3 - 256 a^2 b^9 c^7 x^5 z^3 +
144 a b^10 c^7 x^5 z^3 + 48 a^2 b^8 c^8 x^5 z^3 -
80 a b^9 c^8 x^5 z^3 + 16 a b^8 c^9 x^5 z^3 -
12 a^10 b^6 c^2 x^4 y z^3 + 8 a^9 b^7 c^2 x^4 y z^3 +
68 a^8 b^8 c^2 x^4 y z^3 - 80 a^7 b^9 c^2 x^4 y z^3 -
72 a^6 b^10 c^2 x^4 y z^3 + 128 a^5 b^11 c^2 x^4 y z^3 -
8 a^4 b^12 c^2 x^4 y z^3 - 48 a^3 b^13 c^2 x^4 y z^3 +
20 a^2 b^14 c^2 x^4 y z^3 - 8 a b^15 c^2 x^4 y z^3 +
4 b^16 c^2 x^4 y z^3 - 24 a^9 b^6 c^3 x^4 y z^3 -
120 a^8 b^7 c^3 x^4 y z^3 + 368 a^7 b^8 c^3 x^4 y z^3 -
512 a^5 b^10 c^3 x^4 y z^3 + 208 a^4 b^11 c^3 x^4 y z^3 +
144 a^3 b^12 c^3 x^4 y z^3 - 64 a^2 b^13 c^3 x^4 y z^3 +
24 a b^14 c^3 x^4 y z^3 - 24 b^15 c^3 x^4 y z^3 -
316 a^8 b^6 c^4 x^4 y z^3 + 1072 a^7 b^7 c^4 x^4 y z^3 +
144 a^6 b^8 c^4 x^4 y z^3 - 1536 a^5 b^9 c^4 x^4 y z^3 +
136 a^4 b^10 c^4 x^4 y z^3 + 432 a^3 b^11 c^4 x^4 y z^3 -
16 a^2 b^12 c^4 x^4 y z^3 + 32 a b^13 c^4 x^4 y z^3 +
52 b^14 c^4 x^4 y z^3 - 208 a^7 b^6 c^5 x^4 y z^3 +
3136 a^6 b^7 c^5 x^4 y z^3 + 5376 a^5 b^8 c^5 x^4 y z^3 -
1824 a^4 b^9 c^5 x^4 y z^3 - 1232 a^3 b^10 c^5 x^4 y z^3 +
128 a^2 b^11 c^5 x^4 y z^3 - 224 a b^12 c^5 x^4 y z^3 -
32 b^13 c^5 x^4 y z^3 + 1912 a^6 b^6 c^6 x^4 y z^3 +
4480 a^5 b^7 c^6 x^4 y z^3 + 904 a^4 b^8 c^6 x^4 y z^3 +
432 a^3 b^9 c^6 x^4 y z^3 + 184 a^2 b^10 c^6 x^4 y z^3 +
336 a b^11 c^6 x^4 y z^3 - 56 b^12 c^6 x^4 y z^3 +
256 a^5 b^6 c^7 x^4 y z^3 + 2128 a^4 b^7 c^7 x^4 y z^3 +
624 a^3 b^8 c^7 x^4 y z^3 - 576 a^2 b^9 c^7 x^4 y z^3 -
112 a b^10 c^7 x^4 y z^3 + 112 b^11 c^7 x^4 y z^3 -
1544 a^4 b^6 c^8 x^4 y z^3 - 304 a^3 b^7 c^8 x^4 y z^3 +
368 a^2 b^8 c^8 x^4 y z^3 - 224 a b^9 c^8 x^4 y z^3 -
56 b^10 c^8 x^4 y z^3 - 48 a^3 b^6 c^9 x^4 y z^3 +
288 a b^8 c^9 x^4 y z^3 - 32 b^9 c^9 x^4 y z^3 -
44 a^2 b^6 c^10 x^4 y z^3 - 136 a b^7 c^10 x^4 y z^3 +
52 b^8 c^10 x^4 y z^3 + 24 a b^6 c^11 x^4 y z^3 -
24 b^7 c^11 x^4 y z^3 + 4 b^6 c^12 x^4 y z^3 +
28 a^12 b^4 c^2 x^3 y^2 z^3 - 136 a^11 b^5 c^2 x^3 y^2 z^3 +
204 a^10 b^6 c^2 x^3 y^2 z^3 - 296 a^8 b^8 c^2 x^3 y^2 z^3 +
304 a^7 b^9 c^2 x^3 y^2 z^3 - 104 a^6 b^10 c^2 x^3 y^2 z^3 -
64 a^5 b^11 c^2 x^3 y^2 z^3 + 140 a^4 b^12 c^2 x^3 y^2 z^3 -
104 a^3 b^13 c^2 x^3 y^2 z^3 + 28 a^2 b^14 c^2 x^3 y^2 z^3 +
8 a^11 b^4 c^3 x^3 y^2 z^3 - 216 a^10 b^5 c^3 x^3 y^2 z^3 +
624 a^9 b^6 c^3 x^3 y^2 z^3 - 592 a^8 b^7 c^3 x^3 y^2 z^3 -
64 a^7 b^8 c^3 x^3 y^2 z^3 + 704 a^6 b^9 c^3 x^3 y^2 z^3 -
752 a^5 b^10 c^3 x^3 y^2 z^3 + 208 a^4 b^11 c^3 x^3 y^2 z^3 +
184 a^3 b^12 c^3 x^3 y^2 z^3 - 104 a^2 b^13 c^3 x^3 y^2 z^3 +
844 a^10 b^4 c^4 x^3 y^2 z^3 - 1008 a^9 b^5 c^4 x^3 y^2 z^3 -
848 a^8 b^6 c^4 x^3 y^2 z^3 + 2736 a^7 b^7 c^4 x^3 y^2 z^3 -
1208 a^6 b^8 c^4 x^3 y^2 z^3 - 1936 a^5 b^9 c^4 x^3 y^2 z^3 +
1072 a^4 b^10 c^4 x^3 y^2 z^3 + 208 a^3 b^11 c^4 x^3 y^2 z^3 +
140 a^2 b^12 c^4 x^3 y^2 z^3 - 608 a^9 b^4 c^5 x^3 y^2 z^3 -
464 a^8 b^5 c^5 x^3 y^2 z^3 + 4496 a^7 b^6 c^5 x^3 y^2 z^3 +
6560 a^6 b^7 c^5 x^3 y^2 z^3 + 3008 a^5 b^8 c^5 x^3 y^2 z^3 -
1936 a^4 b^9 c^5 x^3 y^2 z^3 - 752 a^3 b^10 c^5 x^3 y^2 z^3 -
64 a^2 b^11 c^5 x^3 y^2 z^3 - 872 a^8 b^4 c^6 x^3 y^2 z^3 +
1824 a^7 b^5 c^6 x^3 y^2 z^3 + 12552 a^6 b^6 c^6 x^3 y^2 z^3 +
6560 a^5 b^7 c^6 x^3 y^2 z^3 - 1208 a^4 b^8 c^6 x^3 y^2 z^3 +
704 a^3 b^9 c^6 x^3 y^2 z^3 - 104 a^2 b^10 c^6 x^3 y^2 z^3 +
1200 a^7 b^4 c^7 x^3 y^2 z^3 + 1824 a^6 b^5 c^7 x^3 y^2 z^3 +
4496 a^5 b^6 c^7 x^3 y^2 z^3 + 2736 a^4 b^7 c^7 x^3 y^2 z^3 -
64 a^3 b^8 c^7 x^3 y^2 z^3 + 304 a^2 b^9 c^7 x^3 y^2 z^3 -
872 a^6 b^4 c^8 x^3 y^2 z^3 - 464 a^5 b^5 c^8 x^3 y^2 z^3 -
848 a^4 b^6 c^8 x^3 y^2 z^3 - 592 a^3 b^7 c^8 x^3 y^2 z^3 -
296 a^2 b^8 c^8 x^3 y^2 z^3 - 608 a^5 b^4 c^9 x^3 y^2 z^3 -
1008 a^4 b^5 c^9 x^3 y^2 z^3 + 624 a^3 b^6 c^9 x^3 y^2 z^3 +
844 a^4 b^4 c^10 x^3 y^2 z^3 - 216 a^3 b^5 c^10 x^3 y^2 z^3 +
204 a^2 b^6 c^10 x^3 y^2 z^3 + 8 a^3 b^4 c^11 x^3 y^2 z^3 -
136 a^2 b^5 c^11 x^3 y^2 z^3 + 28 a^2 b^4 c^12 x^3 y^2 z^3 +
28 a^14 b^2 c^2 x^2 y^3 z^3 - 104 a^13 b^3 c^2 x^2 y^3 z^3 +
140 a^12 b^4 c^2 x^2 y^3 z^3 - 64 a^11 b^5 c^2 x^2 y^3 z^3 -
104 a^10 b^6 c^2 x^2 y^3 z^3 + 304 a^9 b^7 c^2 x^2 y^3 z^3 -
296 a^8 b^8 c^2 x^2 y^3 z^3 + 204 a^6 b^10 c^2 x^2 y^3 z^3 -
136 a^5 b^11 c^2 x^2 y^3 z^3 + 28 a^4 b^12 c^2 x^2 y^3 z^3 -
104 a^13 b^2 c^3 x^2 y^3 z^3 + 184 a^12 b^3 c^3 x^2 y^3 z^3 +
208 a^11 b^4 c^3 x^2 y^3 z^3 - 752 a^10 b^5 c^3 x^2 y^3 z^3 +
704 a^9 b^6 c^3 x^2 y^3 z^3 - 64 a^8 b^7 c^3 x^2 y^3 z^3 -
592 a^7 b^8 c^3 x^2 y^3 z^3 + 624 a^6 b^9 c^3 x^2 y^3 z^3 -
216 a^5 b^10 c^3 x^2 y^3 z^3 + 8 a^4 b^11 c^3 x^2 y^3 z^3 +
140 a^12 b^2 c^4 x^2 y^3 z^3 + 208 a^11 b^3 c^4 x^2 y^3 z^3 +
1072 a^10 b^4 c^4 x^2 y^3 z^3 - 1936 a^9 b^5 c^4 x^2 y^3 z^3 -
1208 a^8 b^6 c^4 x^2 y^3 z^3 + 2736 a^7 b^7 c^4 x^2 y^3 z^3 -
848 a^6 b^8 c^4 x^2 y^3 z^3 - 1008 a^5 b^9 c^4 x^2 y^3 z^3 +
844 a^4 b^10 c^4 x^2 y^3 z^3 - 64 a^11 b^2 c^5 x^2 y^3 z^3 -
752 a^10 b^3 c^5 x^2 y^3 z^3 - 1936 a^9 b^4 c^5 x^2 y^3 z^3 +
3008 a^8 b^5 c^5 x^2 y^3 z^3 + 6560 a^7 b^6 c^5 x^2 y^3 z^3 +
4496 a^6 b^7 c^5 x^2 y^3 z^3 - 464 a^5 b^8 c^5 x^2 y^3 z^3 -
608 a^4 b^9 c^5 x^2 y^3 z^3 - 104 a^10 b^2 c^6 x^2 y^3 z^3 +
704 a^9 b^3 c^6 x^2 y^3 z^3 - 1208 a^8 b^4 c^6 x^2 y^3 z^3 +
6560 a^7 b^5 c^6 x^2 y^3 z^3 + 12552 a^6 b^6 c^6 x^2 y^3 z^3 +
1824 a^5 b^7 c^6 x^2 y^3 z^3 - 872 a^4 b^8 c^6 x^2 y^3 z^3 +
304 a^9 b^2 c^7 x^2 y^3 z^3 - 64 a^8 b^3 c^7 x^2 y^3 z^3 +
2736 a^7 b^4 c^7 x^2 y^3 z^3 + 4496 a^6 b^5 c^7 x^2 y^3 z^3 +
1824 a^5 b^6 c^7 x^2 y^3 z^3 + 1200 a^4 b^7 c^7 x^2 y^3 z^3 -
296 a^8 b^2 c^8 x^2 y^3 z^3 - 592 a^7 b^3 c^8 x^2 y^3 z^3 -
848 a^6 b^4 c^8 x^2 y^3 z^3 - 464 a^5 b^5 c^8 x^2 y^3 z^3 -
872 a^4 b^6 c^8 x^2 y^3 z^3 + 624 a^6 b^3 c^9 x^2 y^3 z^3 -
1008 a^5 b^4 c^9 x^2 y^3 z^3 - 608 a^4 b^5 c^9 x^2 y^3 z^3 +
204 a^6 b^2 c^10 x^2 y^3 z^3 - 216 a^5 b^3 c^10 x^2 y^3 z^3 +
844 a^4 b^4 c^10 x^2 y^3 z^3 - 136 a^5 b^2 c^11 x^2 y^3 z^3 +
8 a^4 b^3 c^11 x^2 y^3 z^3 + 28 a^4 b^2 c^12 x^2 y^3 z^3 +
4 a^16 c^2 x y^4 z^3 - 8 a^15 b c^2 x y^4 z^3 +
20 a^14 b^2 c^2 x y^4 z^3 - 48 a^13 b^3 c^2 x y^4 z^3 -
8 a^12 b^4 c^2 x y^4 z^3 + 128 a^11 b^5 c^2 x y^4 z^3 -
72 a^10 b^6 c^2 x y^4 z^3 - 80 a^9 b^7 c^2 x y^4 z^3 +
68 a^8 b^8 c^2 x y^4 z^3 + 8 a^7 b^9 c^2 x y^4 z^3 -
12 a^6 b^10 c^2 x y^4 z^3 - 24 a^15 c^3 x y^4 z^3 +
24 a^14 b c^3 x y^4 z^3 - 64 a^13 b^2 c^3 x y^4 z^3 +
144 a^12 b^3 c^3 x y^4 z^3 + 208 a^11 b^4 c^3 x y^4 z^3 -
512 a^10 b^5 c^3 x y^4 z^3 + 368 a^8 b^7 c^3 x y^4 z^3 -
120 a^7 b^8 c^3 x y^4 z^3 - 24 a^6 b^9 c^3 x y^4 z^3 +
52 a^14 c^4 x y^4 z^3 + 32 a^13 b c^4 x y^4 z^3 -
16 a^12 b^2 c^4 x y^4 z^3 + 432 a^11 b^3 c^4 x y^4 z^3 +
136 a^10 b^4 c^4 x y^4 z^3 - 1536 a^9 b^5 c^4 x y^4 z^3 +
144 a^8 b^6 c^4 x y^4 z^3 + 1072 a^7 b^7 c^4 x y^4 z^3 -
316 a^6 b^8 c^4 x y^4 z^3 - 32 a^13 c^5 x y^4 z^3 -
224 a^12 b c^5 x y^4 z^3 + 128 a^11 b^2 c^5 x y^4 z^3 -
1232 a^10 b^3 c^5 x y^4 z^3 - 1824 a^9 b^4 c^5 x y^4 z^3 +
5376 a^8 b^5 c^5 x y^4 z^3 + 3136 a^7 b^6 c^5 x y^4 z^3 -
208 a^6 b^7 c^5 x y^4 z^3 - 56 a^12 c^6 x y^4 z^3 +
336 a^11 b c^6 x y^4 z^3 + 184 a^10 b^2 c^6 x y^4 z^3 +
432 a^9 b^3 c^6 x y^4 z^3 + 904 a^8 b^4 c^6 x y^4 z^3 +
4480 a^7 b^5 c^6 x y^4 z^3 + 1912 a^6 b^6 c^6 x y^4 z^3 +
112 a^11 c^7 x y^4 z^3 - 112 a^10 b c^7 x y^4 z^3 -
576 a^9 b^2 c^7 x y^4 z^3 + 624 a^8 b^3 c^7 x y^4 z^3 +
2128 a^7 b^4 c^7 x y^4 z^3 + 256 a^6 b^5 c^7 x y^4 z^3 -
56 a^10 c^8 x y^4 z^3 - 224 a^9 b c^8 x y^4 z^3 +
368 a^8 b^2 c^8 x y^4 z^3 - 304 a^7 b^3 c^8 x y^4 z^3 -
1544 a^6 b^4 c^8 x y^4 z^3 - 32 a^9 c^9 x y^4 z^3 +
288 a^8 b c^9 x y^4 z^3 - 48 a^6 b^3 c^9 x y^4 z^3 +
52 a^8 c^10 x y^4 z^3 - 136 a^7 b c^10 x y^4 z^3 -
44 a^6 b^2 c^10 x y^4 z^3 - 24 a^7 c^11 x y^4 z^3 +
24 a^6 b c^11 x y^4 z^3 + 4 a^6 c^12 x y^4 z^3 +
16 a^15 b c^2 y^5 z^3 - 48 a^14 b^2 c^2 y^5 z^3 +
16 a^13 b^3 c^2 y^5 z^3 + 80 a^12 b^4 c^2 y^5 z^3 -
80 a^11 b^5 c^2 y^5 z^3 - 16 a^10 b^6 c^2 y^5 z^3 +
48 a^9 b^7 c^2 y^5 z^3 - 16 a^8 b^8 c^2 y^5 z^3 -
80 a^14 b c^3 y^5 z^3 + 128 a^13 b^2 c^3 y^5 z^3 +
176 a^12 b^3 c^3 y^5 z^3 - 384 a^11 b^4 c^3 y^5 z^3 +
16 a^10 b^5 c^3 y^5 z^3 + 256 a^9 b^6 c^3 y^5 z^3 -
112 a^8 b^7 c^3 y^5 z^3 + 144 a^13 b c^4 y^5 z^3 +
16 a^12 b^2 c^4 y^5 z^3 - 352 a^11 b^3 c^4 y^5 z^3 +
32 a^10 b^4 c^4 y^5 z^3 + 208 a^9 b^5 c^4 y^5 z^3 -
48 a^8 b^6 c^4 y^5 z^3 - 80 a^12 b c^5 y^5 z^3 -
384 a^11 b^2 c^5 y^5 z^3 - 416 a^10 b^3 c^5 y^5 z^3 +
768 a^9 b^4 c^5 y^5 z^3 + 1136 a^8 b^5 c^5 y^5 z^3 -
80 a^11 b c^6 y^5 z^3 + 496 a^10 b^2 c^6 y^5 z^3 +
1104 a^9 b^3 c^6 y^5 z^3 - 496 a^8 b^4 c^6 y^5 z^3 +
144 a^10 b c^7 y^5 z^3 - 256 a^9 b^2 c^7 y^5 z^3 -
528 a^8 b^3 c^7 y^5 z^3 - 80 a^9 b c^8 y^5 z^3 +
48 a^8 b^2 c^8 y^5 z^3 + 16 a^8 b c^9 y^5 z^3 + a^10 b^8 x^4 z^4 -
6 a^9 b^9 x^4 z^4 + 13 a^8 b^10 x^4 z^4 - 8 a^7 b^11 x^4 z^4 -
14 a^6 b^12 x^4 z^4 + 28 a^5 b^13 x^4 z^4 - 14 a^4 b^14 x^4 z^4 -
8 a^3 b^15 x^4 z^4 + 13 a^2 b^16 x^4 z^4 - 6 a b^17 x^4 z^4 +
b^18 x^4 z^4 + 10 a^9 b^8 c x^4 z^4 - 54 a^8 b^9 c x^4 z^4 +
104 a^7 b^10 c x^4 z^4 - 56 a^6 b^11 c x^4 z^4 -
84 a^5 b^12 c x^4 z^4 + 140 a^4 b^13 c x^4 z^4 -
56 a^3 b^14 c x^4 z^4 - 24 a^2 b^15 c x^4 z^4 +
26 a b^16 c x^4 z^4 - 6 b^17 c x^4 z^4 - 19 a^8 b^8 c^2 x^4 z^4 +
8 a^7 b^9 c^2 x^4 z^4 + 140 a^6 b^10 c^2 x^4 z^4 -
232 a^5 b^11 c^2 x^4 z^4 + 46 a^4 b^12 c^2 x^4 z^4 +
120 a^3 b^13 c^2 x^4 z^4 - 52 a^2 b^14 c^2 x^4 z^4 -
24 a b^15 c^2 x^4 z^4 + 13 b^16 c^2 x^4 z^4 -
392 a^7 b^8 c^3 x^4 z^4 + 872 a^6 b^9 c^3 x^4 z^4 -
168 a^5 b^10 c^3 x^4 z^4 - 728 a^4 b^11 c^3 x^4 z^4 +
360 a^3 b^12 c^3 x^4 z^4 + 120 a^2 b^13 c^3 x^4 z^4 -
56 a b^14 c^3 x^4 z^4 - 8 b^15 c^3 x^4 z^4 -
494 a^6 b^8 c^4 x^4 z^4 + 716 a^5 b^9 c^4 x^4 z^4 +
334 a^4 b^10 c^4 x^4 z^4 - 728 a^3 b^11 c^4 x^4 z^4 +
46 a^2 b^12 c^4 x^4 z^4 + 140 a b^13 c^4 x^4 z^4 -
14 b^14 c^4 x^4 z^4 + 1788 a^5 b^8 c^5 x^4 z^4 +
716 a^4 b^9 c^5 x^4 z^4 - 168 a^3 b^10 c^5 x^4 z^4 -
232 a^2 b^11 c^5 x^4 z^4 - 84 a b^12 c^5 x^4 z^4 +
28 b^13 c^5 x^4 z^4 - 494 a^4 b^8 c^6 x^4 z^4 +
872 a^3 b^9 c^6 x^4 z^4 + 140 a^2 b^10 c^6 x^4 z^4 -
56 a b^11 c^6 x^4 z^4 - 14 b^12 c^6 x^4 z^4 -
392 a^3 b^8 c^7 x^4 z^4 + 8 a^2 b^9 c^7 x^4 z^4 +
104 a b^10 c^7 x^4 z^4 - 8 b^11 c^7 x^4 z^4 -
19 a^2 b^8 c^8 x^4 z^4 - 54 a b^9 c^8 x^4 z^4 +
13 b^10 c^8 x^4 z^4 + 10 a b^8 c^9 x^4 z^4 - 6 b^9 c^9 x^4 z^4 +
b^8 c^10 x^4 z^4 + 4 a^12 b^6 x^3 y z^4 - 24 a^11 b^7 x^3 y z^4 +
52 a^10 b^8 x^3 y z^4 - 32 a^9 b^9 x^3 y z^4 -
56 a^8 b^10 x^3 y z^4 + 112 a^7 b^11 x^3 y z^4 -
56 a^6 b^12 x^3 y z^4 - 32 a^5 b^13 x^3 y z^4 +
52 a^4 b^14 x^3 y z^4 - 24 a^3 b^15 x^3 y z^4 +
4 a^2 b^16 x^3 y z^4 + 24 a^11 b^6 c x^3 y z^4 -
136 a^10 b^7 c x^3 y z^4 + 288 a^9 b^8 c x^3 y z^4 -
224 a^8 b^9 c x^3 y z^4 - 112 a^7 b^10 c x^3 y z^4 +
336 a^6 b^11 c x^3 y z^4 - 224 a^5 b^12 c x^3 y z^4 +
32 a^4 b^13 c x^3 y z^4 + 24 a^3 b^14 c x^3 y z^4 -
8 a^2 b^15 c x^3 y z^4 - 44 a^10 b^6 c^2 x^3 y z^4 +
368 a^8 b^8 c^2 x^3 y z^4 - 576 a^7 b^9 c^2 x^3 y z^4 +
184 a^6 b^10 c^2 x^3 y z^4 + 128 a^5 b^11 c^2 x^3 y z^4 -
16 a^4 b^12 c^2 x^3 y z^4 - 64 a^3 b^13 c^2 x^3 y z^4 +
20 a^2 b^14 c^2 x^3 y z^4 - 48 a^9 b^6 c^3 x^3 y z^4 -
304 a^8 b^7 c^3 x^3 y z^4 + 624 a^7 b^8 c^3 x^3 y z^4 +
432 a^6 b^9 c^3 x^3 y z^4 - 1232 a^5 b^10 c^3 x^3 y z^4 +
432 a^4 b^11 c^3 x^3 y z^4 + 144 a^3 b^12 c^3 x^3 y z^4 -
48 a^2 b^13 c^3 x^3 y z^4 - 1544 a^8 b^6 c^4 x^3 y z^4 +
2128 a^7 b^7 c^4 x^3 y z^4 + 904 a^6 b^8 c^4 x^3 y z^4 -
1824 a^5 b^9 c^4 x^3 y z^4 + 136 a^4 b^10 c^4 x^3 y z^4 +
208 a^3 b^11 c^4 x^3 y z^4 - 8 a^2 b^12 c^4 x^3 y z^4 +
256 a^7 b^6 c^5 x^3 y z^4 + 4480 a^6 b^7 c^5 x^3 y z^4 +
5376 a^5 b^8 c^5 x^3 y z^4 - 1536 a^4 b^9 c^5 x^3 y z^4 -
512 a^3 b^10 c^5 x^3 y z^4 + 128 a^2 b^11 c^5 x^3 y z^4 +
1912 a^6 b^6 c^6 x^3 y z^4 + 3136 a^5 b^7 c^6 x^3 y z^4 +
144 a^4 b^8 c^6 x^3 y z^4 - 72 a^2 b^10 c^6 x^3 y z^4 -
208 a^5 b^6 c^7 x^3 y z^4 + 1072 a^4 b^7 c^7 x^3 y z^4 +
368 a^3 b^8 c^7 x^3 y z^4 - 80 a^2 b^9 c^7 x^3 y z^4 -
316 a^4 b^6 c^8 x^3 y z^4 - 120 a^3 b^7 c^8 x^3 y z^4 +
68 a^2 b^8 c^8 x^3 y z^4 - 24 a^3 b^6 c^9 x^3 y z^4 +
8 a^2 b^7 c^9 x^3 y z^4 - 12 a^2 b^6 c^10 x^3 y z^4 +
6 a^14 b^4 x^2 y^2 z^4 - 36 a^13 b^5 x^2 y^2 z^4 +
78 a^12 b^6 x^2 y^2 z^4 - 48 a^11 b^7 x^2 y^2 z^4 -
84 a^10 b^8 x^2 y^2 z^4 + 168 a^9 b^9 x^2 y^2 z^4 -
84 a^8 b^10 x^2 y^2 z^4 - 48 a^7 b^11 x^2 y^2 z^4 +
78 a^6 b^12 x^2 y^2 z^4 - 36 a^5 b^13 x^2 y^2 z^4 +
6 a^4 b^14 x^2 y^2 z^4 + 12 a^13 b^4 c x^2 y^2 z^4 -
84 a^12 b^5 c x^2 y^2 z^4 + 240 a^11 b^6 c x^2 y^2 z^4 -
336 a^10 b^7 c x^2 y^2 z^4 + 168 a^9 b^8 c x^2 y^2 z^4 +
168 a^8 b^9 c x^2 y^2 z^4 - 336 a^7 b^10 c x^2 y^2 z^4 +
240 a^6 b^11 c x^2 y^2 z^4 - 84 a^5 b^12 c x^2 y^2 z^4 +
12 a^4 b^13 c x^2 y^2 z^4 - 18 a^12 b^4 c^2 x^2 y^2 z^4 -
48 a^11 b^5 c^2 x^2 y^2 z^4 + 264 a^10 b^6 c^2 x^2 y^2 z^4 -
336 a^9 b^7 c^2 x^2 y^2 z^4 + 276 a^8 b^8 c^2 x^2 y^2 z^4 -
336 a^7 b^9 c^2 x^2 y^2 z^4 + 264 a^6 b^10 c^2 x^2 y^2 z^4 -
48 a^5 b^11 c^2 x^2 y^2 z^4 - 18 a^4 b^12 c^2 x^2 y^2 z^4 +
304 a^11 b^4 c^3 x^2 y^2 z^4 - 976 a^10 b^5 c^3 x^2 y^2 z^4 +
1104 a^9 b^6 c^3 x^2 y^2 z^4 - 432 a^8 b^7 c^3 x^2 y^2 z^4 -
432 a^7 b^8 c^3 x^2 y^2 z^4 + 1104 a^6 b^9 c^3 x^2 y^2 z^4 -
976 a^5 b^10 c^3 x^2 y^2 z^4 + 304 a^4 b^11 c^3 x^2 y^2 z^4 +
492 a^10 b^4 c^4 x^2 y^2 z^4 - 1592 a^9 b^5 c^4 x^2 y^2 z^4 -
876 a^8 b^6 c^4 x^2 y^2 z^4 + 3952 a^7 b^7 c^4 x^2 y^2 z^4 -
876 a^6 b^8 c^4 x^2 y^2 z^4 - 1592 a^5 b^9 c^4 x^2 y^2 z^4 +
492 a^4 b^10 c^4 x^2 y^2 z^4 - 664 a^9 b^4 c^5 x^2 y^2 z^4 +
1032 a^8 b^5 c^5 x^2 y^2 z^4 + 5776 a^7 b^6 c^5 x^2 y^2 z^4 +
5776 a^6 b^7 c^5 x^2 y^2 z^4 + 1032 a^5 b^8 c^5 x^2 y^2 z^4 -
664 a^4 b^9 c^5 x^2 y^2 z^4 - 916 a^8 b^4 c^6 x^2 y^2 z^4 +
1552 a^7 b^5 c^6 x^2 y^2 z^4 + 8072 a^6 b^6 c^6 x^2 y^2 z^4 +
1552 a^5 b^7 c^6 x^2 y^2 z^4 - 916 a^4 b^8 c^6 x^2 y^2 z^4 +
624 a^7 b^4 c^7 x^2 y^2 z^4 + 816 a^6 b^5 c^7 x^2 y^2 z^4 +
816 a^5 b^6 c^7 x^2 y^2 z^4 + 624 a^4 b^7 c^7 x^2 y^2 z^4 +
142 a^6 b^4 c^8 x^2 y^2 z^4 - 388 a^5 b^5 c^8 x^2 y^2 z^4 +
142 a^4 b^6 c^8 x^2 y^2 z^4 - 276 a^5 b^4 c^9 x^2 y^2 z^4 -
276 a^4 b^5 c^9 x^2 y^2 z^4 + 294 a^4 b^4 c^10 x^2 y^2 z^4 +
4 a^16 b^2 x y^3 z^4 - 24 a^15 b^3 x y^3 z^4 +
52 a^14 b^4 x y^3 z^4 - 32 a^13 b^5 x y^3 z^4 -
56 a^12 b^6 x y^3 z^4 + 112 a^11 b^7 x y^3 z^4 -
56 a^10 b^8 x y^3 z^4 - 32 a^9 b^9 x y^3 z^4 +
52 a^8 b^10 x y^3 z^4 - 24 a^7 b^11 x y^3 z^4 +
4 a^6 b^12 x y^3 z^4 - 8 a^15 b^2 c x y^3 z^4 +
24 a^14 b^3 c x y^3 z^4 + 32 a^13 b^4 c x y^3 z^4 -
224 a^12 b^5 c x y^3 z^4 + 336 a^11 b^6 c x y^3 z^4 -
112 a^10 b^7 c x y^3 z^4 - 224 a^9 b^8 c x y^3 z^4 +
288 a^8 b^9 c x y^3 z^4 - 136 a^7 b^10 c x y^3 z^4 +
24 a^6 b^11 c x y^3 z^4 + 20 a^14 b^2 c^2 x y^3 z^4 -
64 a^13 b^3 c^2 x y^3 z^4 - 16 a^12 b^4 c^2 x y^3 z^4 +
128 a^11 b^5 c^2 x y^3 z^4 + 184 a^10 b^6 c^2 x y^3 z^4 -
576 a^9 b^7 c^2 x y^3 z^4 + 368 a^8 b^8 c^2 x y^3 z^4 -
44 a^6 b^10 c^2 x y^3 z^4 - 48 a^13 b^2 c^3 x y^3 z^4 +
144 a^12 b^3 c^3 x y^3 z^4 + 432 a^11 b^4 c^3 x y^3 z^4 -
1232 a^10 b^5 c^3 x y^3 z^4 + 432 a^9 b^6 c^3 x y^3 z^4 +
624 a^8 b^7 c^3 x y^3 z^4 - 304 a^7 b^8 c^3 x y^3 z^4 -
48 a^6 b^9 c^3 x y^3 z^4 - 8 a^12 b^2 c^4 x y^3 z^4 +
208 a^11 b^3 c^4 x y^3 z^4 + 136 a^10 b^4 c^4 x y^3 z^4 -
1824 a^9 b^5 c^4 x y^3 z^4 + 904 a^8 b^6 c^4 x y^3 z^4 +
2128 a^7 b^7 c^4 x y^3 z^4 - 1544 a^6 b^8 c^4 x y^3 z^4 +
128 a^11 b^2 c^5 x y^3 z^4 - 512 a^10 b^3 c^5 x y^3 z^4 -
1536 a^9 b^4 c^5 x y^3 z^4 + 5376 a^8 b^5 c^5 x y^3 z^4 +
4480 a^7 b^6 c^5 x y^3 z^4 + 256 a^6 b^7 c^5 x y^3 z^4 -
72 a^10 b^2 c^6 x y^3 z^4 + 144 a^8 b^4 c^6 x y^3 z^4 +
3136 a^7 b^5 c^6 x y^3 z^4 + 1912 a^6 b^6 c^6 x y^3 z^4 -
80 a^9 b^2 c^7 x y^3 z^4 + 368 a^8 b^3 c^7 x y^3 z^4 +
1072 a^7 b^4 c^7 x y^3 z^4 - 208 a^6 b^5 c^7 x y^3 z^4 +
68 a^8 b^2 c^8 x y^3 z^4 - 120 a^7 b^3 c^8 x y^3 z^4 -
316 a^6 b^4 c^8 x y^3 z^4 + 8 a^7 b^2 c^9 x y^3 z^4 -
24 a^6 b^3 c^9 x y^3 z^4 - 12 a^6 b^2 c^10 x y^3 z^4 +
a^18 y^4 z^4 - 6 a^17 b y^4 z^4 + 13 a^16 b^2 y^4 z^4 -
8 a^15 b^3 y^4 z^4 - 14 a^14 b^4 y^4 z^4 + 28 a^13 b^5 y^4 z^4 -
14 a^12 b^6 y^4 z^4 - 8 a^11 b^7 y^4 z^4 + 13 a^10 b^8 y^4 z^4 -
6 a^9 b^9 y^4 z^4 + a^8 b^10 y^4 z^4 - 6 a^17 c y^4 z^4 +
26 a^16 b c y^4 z^4 - 24 a^15 b^2 c y^4 z^4 -
56 a^14 b^3 c y^4 z^4 + 140 a^13 b^4 c y^4 z^4 -
84 a^12 b^5 c y^4 z^4 - 56 a^11 b^6 c y^4 z^4 +
104 a^10 b^7 c y^4 z^4 - 54 a^9 b^8 c y^4 z^4 +
10 a^8 b^9 c y^4 z^4 + 13 a^16 c^2 y^4 z^4 - 24 a^15 b c^2 y^4 z^4 -
52 a^14 b^2 c^2 y^4 z^4 + 120 a^13 b^3 c^2 y^4 z^4 +
46 a^12 b^4 c^2 y^4 z^4 - 232 a^11 b^5 c^2 y^4 z^4 +
140 a^10 b^6 c^2 y^4 z^4 + 8 a^9 b^7 c^2 y^4 z^4 -
19 a^8 b^8 c^2 y^4 z^4 - 8 a^15 c^3 y^4 z^4 -
56 a^14 b c^3 y^4 z^4 + 120 a^13 b^2 c^3 y^4 z^4 +
360 a^12 b^3 c^3 y^4 z^4 - 728 a^11 b^4 c^3 y^4 z^4 -
168 a^10 b^5 c^3 y^4 z^4 + 872 a^9 b^6 c^3 y^4 z^4 -
392 a^8 b^7 c^3 y^4 z^4 - 14 a^14 c^4 y^4 z^4 +
140 a^13 b c^4 y^4 z^4 + 46 a^12 b^2 c^4 y^4 z^4 -
728 a^11 b^3 c^4 y^4 z^4 + 334 a^10 b^4 c^4 y^4 z^4 +
716 a^9 b^5 c^4 y^4 z^4 - 494 a^8 b^6 c^4 y^4 z^4 +
28 a^13 c^5 y^4 z^4 - 84 a^12 b c^5 y^4 z^4 -
232 a^11 b^2 c^5 y^4 z^4 - 168 a^10 b^3 c^5 y^4 z^4 +
716 a^9 b^4 c^5 y^4 z^4 + 1788 a^8 b^5 c^5 y^4 z^4 -
14 a^12 c^6 y^4 z^4 - 56 a^11 b c^6 y^4 z^4 +
140 a^10 b^2 c^6 y^4 z^4 + 872 a^9 b^3 c^6 y^4 z^4 -
494 a^8 b^4 c^6 y^4 z^4 - 8 a^11 c^7 y^4 z^4 +
104 a^10 b c^7 y^4 z^4 + 8 a^9 b^2 c^7 y^4 z^4 -
392 a^8 b^3 c^7 y^4 z^4 + 13 a^10 c^8 y^4 z^4 -
54 a^9 b c^8 y^4 z^4 - 19 a^8 b^2 c^8 y^4 z^4 - 6 a^9 c^9 y^4 z^4 +
10 a^8 b c^9 y^4 z^4 + a^8 c^10 y^4 z^4 + 16 a^9 b^8 c x^3 z^5 -
80 a^8 b^9 c x^3 z^5 + 144 a^7 b^10 c x^3 z^5 -
80 a^6 b^11 c x^3 z^5 - 80 a^5 b^12 c x^3 z^5 +
144 a^4 b^13 c x^3 z^5 - 80 a^3 b^14 c x^3 z^5 +
16 a^2 b^15 c x^3 z^5 + 48 a^8 b^8 c^2 x^3 z^5 -
256 a^7 b^9 c^2 x^3 z^5 + 496 a^6 b^10 c^2 x^3 z^5 -
384 a^5 b^11 c^2 x^3 z^5 + 16 a^4 b^12 c^2 x^3 z^5 +
128 a^3 b^13 c^2 x^3 z^5 - 48 a^2 b^14 c^2 x^3 z^5 -
528 a^7 b^8 c^3 x^3 z^5 + 1104 a^6 b^9 c^3 x^3 z^5 -
416 a^5 b^10 c^3 x^3 z^5 - 352 a^4 b^11 c^3 x^3 z^5 +
176 a^3 b^12 c^3 x^3 z^5 + 16 a^2 b^13 c^3 x^3 z^5 -
496 a^6 b^8 c^4 x^3 z^5 + 768 a^5 b^9 c^4 x^3 z^5 +
32 a^4 b^10 c^4 x^3 z^5 - 384 a^3 b^11 c^4 x^3 z^5 +
80 a^2 b^12 c^4 x^3 z^5 + 1136 a^5 b^8 c^5 x^3 z^5 +
208 a^4 b^9 c^5 x^3 z^5 + 16 a^3 b^10 c^5 x^3 z^5 -
80 a^2 b^11 c^5 x^3 z^5 - 48 a^4 b^8 c^6 x^3 z^5 +
256 a^3 b^9 c^6 x^3 z^5 - 16 a^2 b^10 c^6 x^3 z^5 -
112 a^3 b^8 c^7 x^3 z^5 + 48 a^2 b^9 c^7 x^3 z^5 -
16 a^2 b^8 c^8 x^3 z^5 + 48 a^11 b^6 c x^2 y z^5 -
240 a^10 b^7 c x^2 y z^5 + 432 a^9 b^8 c x^2 y z^5 -
240 a^8 b^9 c x^2 y z^5 - 240 a^7 b^10 c x^2 y z^5 +
432 a^6 b^11 c x^2 y z^5 - 240 a^5 b^12 c x^2 y z^5 +
48 a^4 b^13 c x^2 y z^5 + 48 a^10 b^6 c^2 x^2 y z^5 -
384 a^9 b^7 c^2 x^2 y z^5 + 1008 a^8 b^8 c^2 x^2 y z^5 -
1152 a^7 b^9 c^2 x^2 y z^5 + 528 a^6 b^10 c^2 x^2 y z^5 -
48 a^4 b^12 c^2 x^2 y z^5 - 272 a^9 b^6 c^3 x^2 y z^5 +
80 a^8 b^7 c^3 x^2 y z^5 + 352 a^7 b^8 c^3 x^2 y z^5 +
416 a^6 b^9 c^3 x^2 y z^5 - 848 a^5 b^10 c^3 x^2 y z^5 +
272 a^4 b^11 c^3 x^2 y z^5 - 1552 a^8 b^6 c^4 x^2 y z^5 +
2176 a^7 b^7 c^4 x^2 y z^5 + 352 a^6 b^8 c^4 x^2 y z^5 -
1024 a^5 b^9 c^4 x^2 y z^5 + 48 a^4 b^10 c^4 x^2 y z^5 +
400 a^7 b^6 c^5 x^2 y z^5 + 2480 a^6 b^7 c^5 x^2 y z^5 +
1520 a^5 b^8 c^5 x^2 y z^5 - 560 a^4 b^9 c^5 x^2 y z^5 +
1424 a^6 b^6 c^6 x^2 y z^5 + 768 a^5 b^7 c^6 x^2 y z^5 -
80 a^4 b^8 c^6 x^2 y z^5 - 176 a^5 b^6 c^7 x^2 y z^5 +
240 a^4 b^7 c^7 x^2 y z^5 + 80 a^4 b^6 c^8 x^2 y z^5 +
48 a^13 b^4 c x y^2 z^5 - 240 a^12 b^5 c x y^2 z^5 +
432 a^11 b^6 c x y^2 z^5 - 240 a^10 b^7 c x y^2 z^5 -
240 a^9 b^8 c x y^2 z^5 + 432 a^8 b^9 c x y^2 z^5 -
240 a^7 b^10 c x y^2 z^5 + 48 a^6 b^11 c x y^2 z^5 -
48 a^12 b^4 c^2 x y^2 z^5 + 528 a^10 b^6 c^2 x y^2 z^5 -
1152 a^9 b^7 c^2 x y^2 z^5 + 1008 a^8 b^8 c^2 x y^2 z^5 -
384 a^7 b^9 c^2 x y^2 z^5 + 48 a^6 b^10 c^2 x y^2 z^5 +
272 a^11 b^4 c^3 x y^2 z^5 - 848 a^10 b^5 c^3 x y^2 z^5 +
416 a^9 b^6 c^3 x y^2 z^5 + 352 a^8 b^7 c^3 x y^2 z^5 +
80 a^7 b^8 c^3 x y^2 z^5 - 272 a^6 b^9 c^3 x y^2 z^5 +
48 a^10 b^4 c^4 x y^2 z^5 - 1024 a^9 b^5 c^4 x y^2 z^5 +
352 a^8 b^6 c^4 x y^2 z^5 + 2176 a^7 b^7 c^4 x y^2 z^5 -
1552 a^6 b^8 c^4 x y^2 z^5 - 560 a^9 b^4 c^5 x y^2 z^5 +
1520 a^8 b^5 c^5 x y^2 z^5 + 2480 a^7 b^6 c^5 x y^2 z^5 +
400 a^6 b^7 c^5 x y^2 z^5 - 80 a^8 b^4 c^6 x y^2 z^5 +
768 a^7 b^5 c^6 x y^2 z^5 + 1424 a^6 b^6 c^6 x y^2 z^5 +
240 a^7 b^4 c^7 x y^2 z^5 - 176 a^6 b^5 c^7 x y^2 z^5 +
80 a^6 b^4 c^8 x y^2 z^5 + 16 a^15 b^2 c y^3 z^5 -
80 a^14 b^3 c y^3 z^5 + 144 a^13 b^4 c y^3 z^5 -
80 a^12 b^5 c y^3 z^5 - 80 a^11 b^6 c y^3 z^5 +
144 a^10 b^7 c y^3 z^5 - 80 a^9 b^8 c y^3 z^5 +
16 a^8 b^9 c y^3 z^5 - 48 a^14 b^2 c^2 y^3 z^5 +
128 a^13 b^3 c^2 y^3 z^5 + 16 a^12 b^4 c^2 y^3 z^5 -
384 a^11 b^5 c^2 y^3 z^5 + 496 a^10 b^6 c^2 y^3 z^5 -
256 a^9 b^7 c^2 y^3 z^5 + 48 a^8 b^8 c^2 y^3 z^5 +
16 a^13 b^2 c^3 y^3 z^5 + 176 a^12 b^3 c^3 y^3 z^5 -
352 a^11 b^4 c^3 y^3 z^5 - 416 a^10 b^5 c^3 y^3 z^5 +
1104 a^9 b^6 c^3 y^3 z^5 - 528 a^8 b^7 c^3 y^3 z^5 +
80 a^12 b^2 c^4 y^3 z^5 - 384 a^11 b^3 c^4 y^3 z^5 +
32 a^10 b^4 c^4 y^3 z^5 + 768 a^9 b^5 c^4 y^3 z^5 -
496 a^8 b^6 c^4 y^3 z^5 - 80 a^11 b^2 c^5 y^3 z^5 +
16 a^10 b^3 c^5 y^3 z^5 + 208 a^9 b^4 c^5 y^3 z^5 +
1136 a^8 b^5 c^5 y^3 z^5 - 16 a^10 b^2 c^6 y^3 z^5 +
256 a^9 b^3 c^6 y^3 z^5 - 48 a^8 b^4 c^6 y^3 z^5 +
48 a^9 b^2 c^7 y^3 z^5 - 112 a^8 b^3 c^7 y^3 z^5 -
16 a^8 b^2 c^8 y^3 z^5 + 64 a^8 b^8 c^2 x^2 z^6 -
256 a^7 b^9 c^2 x^2 z^6 + 384 a^6 b^10 c^2 x^2 z^6 -
256 a^5 b^11 c^2 x^2 z^6 + 64 a^4 b^12 c^2 x^2 z^6 -
256 a^7 b^8 c^3 x^2 z^6 + 512 a^6 b^9 c^3 x^2 z^6 -
256 a^5 b^10 c^3 x^2 z^6 - 128 a^6 b^8 c^4 x^2 z^6 +
256 a^5 b^9 c^4 x^2 z^6 - 128 a^4 b^10 c^4 x^2 z^6 +
256 a^5 b^8 c^5 x^2 z^6 + 64 a^4 b^8 c^6 x^2 z^6 +
128 a^10 b^6 c^2 x y z^6 - 512 a^9 b^7 c^2 x y z^6 +
768 a^8 b^8 c^2 x y z^6 - 512 a^7 b^9 c^2 x y z^6 +
128 a^6 b^10 c^2 x y z^6 - 256 a^9 b^6 c^3 x y z^6 +
256 a^8 b^7 c^3 x y z^6 + 256 a^7 b^8 c^3 x y z^6 -
256 a^6 b^9 c^3 x y z^6 - 512 a^8 b^6 c^4 x y z^6 +
1024 a^7 b^7 c^4 x y z^6 - 512 a^6 b^8 c^4 x y z^6 +
256 a^7 b^6 c^5 x y z^6 + 256 a^6 b^7 c^5 x y z^6 +
384 a^6 b^6 c^6 x y z^6 + 64 a^12 b^4 c^2 y^2 z^6 -
256 a^11 b^5 c^2 y^2 z^6 + 384 a^10 b^6 c^2 y^2 z^6 -
256 a^9 b^7 c^2 y^2 z^6 + 64 a^8 b^8 c^2 y^2 z^6 -
256 a^10 b^5 c^3 y^2 z^6 + 512 a^9 b^6 c^3 y^2 z^6 -
256 a^8 b^7 c^3 y^2 z^6 - 128 a^10 b^4 c^4 y^2 z^6 +
256 a^9 b^5 c^4 y^2 z^6 - 128 a^8 b^6 c^4 y^2 z^6 +
256 a^8 b^5 c^5 y^2 z^6 + 64 a^8 b^4 c^6 y^2 z^6

Points on the Locus:

The circumcenter O is on the locus.
The barycentrics of the perspector are:

{a (a^4 - 2 a^2 b^2 + b^4 - a^2 b c + b^3 c - 2 a^2 c^2 - 4 b^2 c^2 + b c^3 + c^4 + 2 a b S - 2 b^2 S + 2 a c S + 4 b c S - 2 c^2 S),
b (a^4 - 2 a^2 b^2 + b^4 + a^3 c - a b^2 c - 4 a^2 c^2 - 2 b^2 c^2 + a c^3 + c^4 - 2 a^2 S + 2 a b S + 4 a c S + 2 b c S - 2 c^2 S),
c (a^4 + a^3 b - 4 a^2 b^2 + a b^3 + b^4 - 2 a^2 c^2 - a b c^2 - 2 b^2 c^2 + c^4 - 2 a^2 S + 4 a b S - 2 b^2 S + 2 a c S +
2 b c S)}

where S is twice the area of ABC, not in ETC, perhaps a simpler form is possible.

ΠΡΟΣΘΗΚΗ 5/9/19
The point with its "brother" are now in ETC
X(34215)= X(4)X(175)∩X(8)X(492)
X(34216)= X(4)X(176)∩X(8)X(491)

INRADIUS 3

Let ABC be a triangle D a point on BC and r_1,r_2 the inradii of ABD, ACD resp. To construct ABC if we know the angles of ABC and are given the r_1,r_2.

Solution:

Let AE = h_a be the altitude from A and r the inradius of ABC.

We have:

h_a = 2r_1r_2 / (r_1 + r_2 - r)

(by this Theorem)

and

r / h_a = 4Rsin(A/2)sin(B/2)sin(C/2)/2RsinBsinC = sin(A/2)/2cos(B/2)cos(C/2)

==> h_a is known.

Addendum (12-1-2011):

Synthetic solution by Nikolaos Dergiades:
Hyacinthos, Message 19725

NO COMPUTATIONS, PLEASE! -- 1

Problem:

Let ABC be a triangle, P a point, A'B'C' the pedal triangle of P and Ab, Ac the orthogonal projections of A' on PB',PC', resp. The line AbAc intersects BC at A". Similarly B' and C'. Which is the locus of P such that the points A',B',C' are collinear?

Lemma:

Let BC be a line segment, A' a fixed point on BC and A a variable point on the perpendicular to BC at A'. Let Ab,Ac be the orthogonal projections of A' on AB,AC, resp. The line AbAc passes through a fixed point.

Let A" be the intersection of the lines BC and AbAc.

We have that:

A"B/A"C = (A'B/A'C)^2 (the proof is left to the reader).

Therefore AbAc passes through the fixed point A".

Now, in the Problem we have:

A"B/A"C = (A'B/A'C)^2

and similarly:

B"C/C"A = (B'C/B'A)^2

C"A/A"B = (C'A/C'B)^2

A",B",C" are collinear ==>

(A"B/A"C).(B"C/C"A).(C"A/A"B) = [(A'B/A'C).(B'C/B'A).(C'A/C'B)]^2 = 1

==>

1. (A'B/A'C).(B'C/B'A).(C'A/C'B) = -1 ==> ABC, A'B'C' are perspective
(ie AA',BB',CC' are concurrent, by Ceva Theorem)

Or

2. (A'B/A'C).(B'C/B'A).(C'A/C'B) = +1 ==> A',B',C' are collinear (by Menelaus Theorem).

1: The locus is the Darboux cubic
2: The locus is the Circumcircle + the Line at Infinity.

Therefore the locus of P is the union of the Darboux cubic, the Circumcircle, and the Line at Infinity.

A CONFIGURATION

Let ABC be a triangle and P a point.

The circle (B, BP) intersects AB at Ac1 (between A,B) and Ac2 (on the extension of BA) AND BC at A1c (between B,C) and A2c (on the extension of BC). The circle (C, CP) intersects AC at Ab1 (between A,C) and Ab2 AND BC at A1b (between B,C) and A2b (on the extension of CB).

1. The lines Ab1Ac2 and Ac1Ab2 intersect at A1.

2. The lines Ab1A1c and Ac1A1b intersect at A2

3. The lines Ab1A1b and Ac1A1c intersect at A3.

4. The lines Ab1A2b and Ac1A2c intersect at A4.

5. The lines Ab1A2c and Ac1A2b intersect at A5.

6. The lines Ab2A1b and Ac2A1c intersect at A6.

7. The lines Ab2A1c and Ac2A1b intersect at A7.

8. The lines Ab2A2b and Ac2A2c intersect at A8.

9. The lines Ab2A2c and Ac2A2b intersect at A9.

10. The lines Ab2A2c and Ab1Ac1 intersect at A10.

Similarly Bi, Ci, i=1,2,...,10

Problem:

Which are the loci of P such that ABC, AiBiCi (i = 1,2,...10)
are perspective?

For i = 1, the locus is the Neuberg cubic (see Hyacinthos, Message 19680 by Francisco Javier García Capitán)

Addendum (12-1-2011)

For i = 2:
A2B2C2 and ABC are never perspective by calculation. In this case the calculations (that consist of a determinant of the three lines is always 1)
Francisco Javier García Capitán

For i = 3 See THIS

Point secAsec(B-C) :: (in trilinears)

Let ABC be a triangle and H its orthocenter.

Define

Ab : the intersection of the parallel from C to AH and the parallel from A to CH (ie AHCAb is parallelogram)

Ac : the intersection of the parallel from B to AH and the parallel from A to BH (ie AHBAc is parallelogram)

The circle (B, BAc) intersects AB at Ac1 (between A,B) and Ac2 and the circle (C, CAb) intersects AC at Ab1 (between A,C) and Ab2.

The lines Ab1Ac2 and Ac1Ab2 intersect at A1.

Similarly the points B1, C1.

The triangles ABC, A1B1C1 are perspective (ie the lines AA1,BB1,CC1 are concurrent).

Proof

We have:

sin(A1AB) / sin(A1AC) = (AAb1 / AAc1).(AAb2 / AAc2).(Ac1Ac2 / Ab1Ab2)
(See THIS)

CAb1 = CAb2 = BAc1 = BAc2 = AH = 2RcosA

AAb1 = AC - CAb1 = 2R(sinB - cosA)

AAc1 = AB - BAc1 = 2R(sinC - cosA)

AAb2 = AC + CAb2 = 2R(sinB + cosA)

AAc2 = AB + BAc2 = 2R(sinC + cosA)

Ac1Ac2 = Ab1Ab2 [= 4RcosA]

==>


sin(A1AB)/sin(A1AC) = [(sinB - cosA)/(sinC - cosA)].[(sinB + cosA)/(sinC + cosA)] =

= ((sinB)^2 - (cosA)^2)/((sinC)^2 - (cosA)^2) =

= (1 - [(cosB)^2 + (cosA)^2]) / (1 - [(cosC)^2 + (cosA)^2])

Cyclically:

sin(B1BC) / sin(B1BA) = ...

sin(C1BA) / sin(C1CB) = ...

By multiplying them we get 1, therefore the lines AA1,BB1,CC1 are concurrent.

The trilinears of the point of concurrence (perspector of the triangles) are:

( 1 / (1 - [(cosB)^2 + (cosC)^2]) :: = 1 / (cos2B + cos2C) :: =

= 1 / cosAcos(B-C) :: = secAsec(B-C) ::

Note: We used figure of acute triangle. The case of non-acute triangle is left to the reader.

CORRECTION:

The trilinears of the point of concurrence (perspector of the triangles) are:

((1 - [(cosB)^2 + (cosC)^2]) :: = (cos2B + cos2C) :: =

= cosAcos(B-C) ::

See the Hyacinthos discussion HERE

INRADIUS 2

To construct triangle ABC if are given the radii r_1, r_2, r_3, defined
as follows: Let Da be a point on BC such that inradius of ABDa = inradius of ACDa := r_1. Similarly r_2, r_3


Solution

Let ABC be the triangle, Da, Db, Dc, three points on BC,CA,AB, resp. such that: inradius of ABDa = inradius of ACDa = r_1, and similarly Db,Dc and AHa := h_a, BH_b : = h_b, CH_c := h_c the three altitudes of ABC and r its inradius.

By this Theorem we have:

h_a = 2(r_1)^2 / (2r_1 - r) ==>

1/h_a = (2r_1 - r) / 2(r_1)^2

and similarly:

1/h_b = (2r_2 - r) / 2(r_2)^2

1/h_c = (2r_3 - r) / 2(r_3)^2

Now, since

1/r = 1/h_a + 1/h_b + 1/h_c

we have:

1/r = [(2r_1 - r) / 2(r_1)^2 ] + [(2r_2 - r) / 2(r_2)^2] + [(2r_3 - r) / 2(r_3)^2]

==>

r^2(1/(r_1)^2 + 1/(r_2)^2 + 1/(r_3)^2) - 2r(1/r_1 + 1/r_2 + 1/r_3) + 2 = 0

==> r is known ==> h_a, h_b, h_c are known (from the formulae above).

So we have to construct triangle ABC whose the three altitudes are known.
It's an easy problem.

CONCURRENT LINES (a configuration)

Let ABC be a triangle.

Denote:
Ac1, Ac2 two points on the line AB such that Ac1 is between A,B and B is between Ac1,Ac2 (ie Ac2 is on the extension of the line segment AB near to B).

Ab1, Ab2 two points on the line AC such that Ab1 is between A,C and C is between Ab1,Ab2 (Ab2 is on the extension of the line segment AC near to C).

Let A1 be the intersection of the lines Ab1Ac2 and Ab2Ac1.

Similarly we define the points B1 and C1.

Problem:

To find a condition in order to be the triangles ABC, A1B1C1 perspective.
(ie to be the lines AA1, BB1, CC1 concurrent).

Solution:

Note: I take the line segments and the angles as unsigned.

AA1, BB1, CC1 are concurrent <==>

sin(A1AB)/sin(A1AC).Cyclically = 1
(Trigonometric version of Ceva Theorem).

Let A* be the intersection of AA1 and Ac2Ab2.

We have :

In the triangle AA*Ac2 by the Law of the sines:

sin(A1AB) / A*Ac2 = sin(AA*Ac2) / AAc2

In the triangle AA*Ab2:

sin(A1AC) / A*Ab2 = sin(AA*Ab2) / AAb2

From these we get (since AA*Ac2 + AA*Ab2 = Pi):

sin(A1AB) / sin(A1AC) = (A*Ac2 / A*Ab2).(AAb2 / AAc2) (1)

We have in the triangle AAc2AAb2 by Ceva Theorem:

(AAc1 / Ac1Ac2) . (Ac2A* / A*Ab2).(Ab2Ab1 / Ab1A) = 1

==>

Ac2A* / A*Ab2 = (Ac1Ac2 / AAc1).(Ab1A / Ab2Ab1)

So the (1) becomes:

sin(A1AB) / sin(A1AC) = (AAb1 / AAc1).(AAb2 / AAc2).(Ac1Ac2 / Ab1Ab2) (2)

Cyclically

sin(B1BC) / sin(B1BA) = (BBc1 / BBa1).(BBc2 / BBa2).(Ba1Ba2 / Bc1Bc2)

sin(C1BA) / sin(C1CB) = (CCa1 / CCb1).(CCa2 / CCb2).(Cb1Cb2 / Ca1Ca2)

Therefore

AA1, BB1, CC1 : concurrent <==>

(AAb1 / AAc1).(AAb2 / AAc2).(Ac1Ac2 / Ab1Ab2).
(BBc1 / BBa1).(BBc2 / BBa2).(Ba1Ba2 / Bc1Bc2).
(CCa1 / CCb1).(CCa2 / CCb2).(Cb1Cb2 / Ca1Ca2) = 1

Exercises for the reader:

1. Let A2 be the intersection of the lines BAb1 and CAc1 (and similarly B2,C2) and A3 the intersection of the lines BAb2 and CAc2 (and similarly B3,C3).

Find conditions in order to be concurrent the lines:

(i) AA2, BB2, CC2 - (ii) AA3, BB3,CC3

2. Investigate the other possible positions of the points Ac1, Ac2 on AB and Ab1,Ab2 on AC etc.

Application:
[Reference: APH, Hyacinthos message #1663]

Let AHa, AHb, AHc be the altitudes of acute ABC.

The circle (B,BHa) intersects AB at Ac1 (between A,B) and Ac2.
The circle (C,CHa) intersects AC at Ab1 (between A,C) and Ab2.

Let A1 be the intersection of Ab1Ac2 and Ac1Ab2.
Similarly B1, C1.

The lines AA1, BB1, CC1 are concurrent.

Proof:

We have:

BAc1 = BAc2 = BHa = c.cosB ==>

AAc1 = c - c.cosB = c(1-cosB)

AAc2 = AB + Ac2 = c + c.cosB = c(1+cosB)

Ac1Ac2 = BAc1 + BAc2 = 2c.cosB

And

CAb1 = CAb2 = CHa = b.cosC ==>

AAb1 = b - b.cosC = b(1-cosC)

AAb2 = AC + Ab2 = b + b.cosC = b(1+cosC)

Ab1Ab2 = CAb1 + CAb2 = 2b.cosC

The (2) above

sin(A1AB) / sin(A1AC) = (AAb1 / AAc1).(AAb2 / AAc2).(Ac1Ac2 / Ab1Ab2)

becomes:

sin(A1AB) / sin(A1AC) =

[b(1-cosC)/c(1-cosB)].[b(1+cosC)/c(1+cosB)].[2c.cosB/2b.cosC] =

[b/c].[(1-cosC)/(1-cosB)].[(1+cosC)/(1+cosB)]*[cosB/cosC] =

[sinB/sinC].[(1-cosC)/(1-cosB)].[(1+cosC)/(1+cosB)].[cosB/cosC]

Similarly

sin(B1BC) / sin(B1BA) = ...

sin(C1BA) / sin(C1CB) = ...

By multiplying them we get 1. Therefore the lines lines AA1, BB1, CC1 are concurrent.

Trilinears:

From sin(A1AB) / sin(A1AC) =
[sinB/sinC].[(1-cosC)/(1-cosB)].[(1+cosC)/(1+cosB)].[cosB/cosC]

we get the 1st trilinear:

(1/sinA).(1-cosA).(1+cosA).(1/cosA) =

(1/sinA).(1-(cosA)^2).(1/cosA) =

(1/sinA).((sinA)^2).(1/cosA) = sinA / cosA = tanA

Exercise: Prove it for ABC non-acute.